Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 28
No circuito da Figura , determine o valor de que resultará na máxima transferência de potência para a carga de .
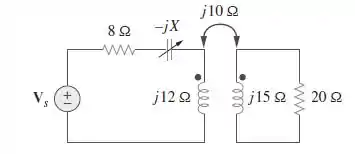
Passo 1
Galera, da teoria nós sabemos que:
Isso significa que para a máxima transferência de potência para uma carga puramente resistiva, a impedância da carga é igual ao módul oda impedância de Thevenin. Portanto, nós vamos obter a impedância de Thevenin vista pelo resistor de e depois vamos usar a relação acima para obter o valor de .
Assim, vamos aplicar a lei das malhas, iniciando pela malha da esquerda:
Para a malha da direita,
Substituindo em , temos:
Passo 2
A impedância de Thevenin é igual a:
Para a máxima transferência de potência,
Resolvendo a equação de segundo grau, temos:
Vamos substituir esses valores na equação para encontrarmos o valor certo de :
Resposta
assume os seguintes valores: