Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 2.Problemas - Ex. 41
Se no circuito da figura , determine .
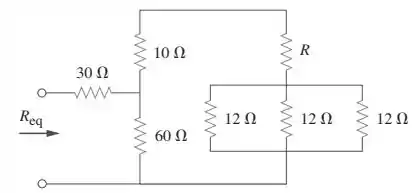
Passo 1
Bora lá! Dá uma olhadinha nesse circuito: vou destacar dois pontos nele.
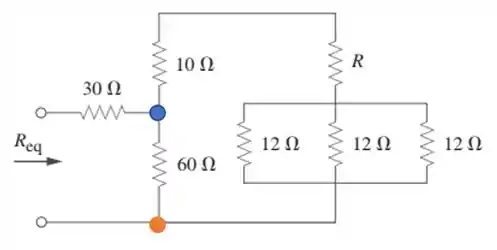
Entre esses dois pontos, azul e laranja, temos dois “fios” sendo ligados: o que desce com o resistor de e o que contorna, com o resistor de , o e os de ; quer dizer que esses dois estão em paralelo. Primeiro, vamos simplificar esse fio que dá a volta: temos três resistores de em paralelo, que vão equivaler a
E portanto, esse lado todo, que está em série, vai ser:
Passo 2
Calculando o paralelo desse lado com o resistor de :
Por fim, essa equivalência está em série com o resistor de , portanto a será:
Passo 3
Como a é :
Multiplicando cruzado,
Portanto,
Resposta
Exercícios de Livros Relacionados
69. Um voltímetro é usado para medir V 0 no circuito da Figura 2.129 . O modelo do voltímetro consiste em um voltímetro ideal em paralelo com um resistor de 100k Ω . Digamos que V s = 40V , R s = 10k
71. A Figura 2.131 representa um modelo de um painel solar fotovoltaico. Dado que V s = 30V , R 1 = 20Ω e i L = 1A , determine R L .
72. Calcule V 0 no circuito divisor de potência bidirecional na Figura 2.132.
74. O circuito da Figura 2.134 destina-se a controlar a velocidade de um motor de modo que ele absorva correntes de 5A , 3A e 1A , quando a chave se encontrar nas posições alta, média e baixa, respect
73. Um modelo de amperímetro consiste em um amperímetro ideal em série com um resistor de 20Ω . Ele é conectado com uma fonte de corrente e um resistor desconhecido R x , como mostra a Figura 2.133 .