Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 2.Problemas - Ex. 24
Para o circuito da figura , determine em termos de , , , e . Se , qual o valor de que produzirá ?
Passo 1
Analisa o circuito:
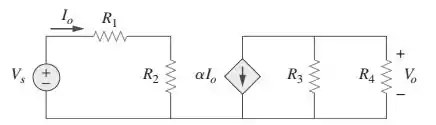
Para resolver essa questão, vamos usar a lei de Kirchoff para tensões. O que a gente vai fazer é o seguinte: vamos caminhar pelo circuito somando e subtraindo tensões e voltar para o mesmo ponto. Qual é a diferença de tensão entre um ponto e ele mesmo? Só pode ser zero! Lembra do seguinte: se passar do menos pro mais na fonte de tensão, soma a tensão, e se passar do mais pro menos, subtrai. Além disso, se a gente passar a favor da corrente no resistor, a tensão abaixa, e se passar contra a corrente, ela aumenta. Repara também no seguinte: o lado esquerdo e o lado direito desse circuito são independentes! Não há passagem de corrente nem de tensão de um lado para o outro.
Passo 2
Do lado esquerdo, temos uma resistência equivalente dos dois resistores em série, assim:
Show, agora no lado esquerdo temos uma resistência equivalente de resistores em paralelo! Repara que a tensão desse lado é , já que os resistores em paralelo têm a mesma tensão.
Portanto, dividindo as equações:
Cortando o que dá pra cortar:
Passo 3
Agora supondo que as resistências todas são iguais, digamos, a um valor , qual produz ?
Portanto,