Para o circuito da Figura 7.98, determine quando e .
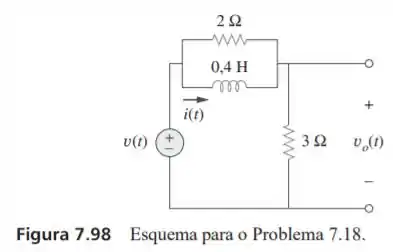
Passo 1
Nosso circuito fica mais simples se percebemos que as duas resistências estão em paralelo, onde, teremos a resistência equivalente sendo dada por
Dessa forma, nossa constante de tempo (para um circuito para um circuito ) será
Com essas informações e com o que foi fornecido no enunciado poderemos elaborar uma expressão para que será
Passo 2
Agora, portanto, podemos concluir nosso exercício fazendo