Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas - Ex. 23

Considere o circuito da Figura 7.103. Dado que v 0 0 = 10   V , determine v 0 e v x para t > 0 .

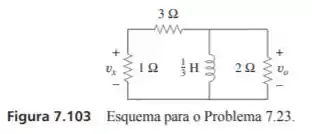
Passo 1

Pela análise do circuito vemos que o resistor de 1 Ω , o resistor equivalente de 4 Ω (soma dos dois resistores em série) e o indutor estão todos em paralelo o que significa que estão sobre uma mesma diferença de potencial. Assim, podemos obter a condição inicial para a corrente que será dada por

- i = 10 2 + 10 3 + 1 → i = - 7 . 5 → i 0 = - 7 . 5   A

Além disso, temos que a resistência de Thevenin observada pelos terminais do indutor é dada por

R t h = 2 ⋅ 4 2 + 4 = 8 6 = 4 3 Ω

Passo 2

Com essas informações conseguimos encontrar nossa constante de tempo que será dada por

τ = L R = 1 3 4 3 = 1 4

Agora ficou simples de concluirmos nosso exercício tendo em vista que podemos equacionar uma expressão para a corrente que será dada por

i t = i 0 ⋅ e - t τ = - 7 . 5 ⋅ e - 4 t ,     t > 0

Assim, a tensão no indutor vai ser dado por

v l = v 0 = l ⋅ d i d t = - 7 . 5 ⋅ - 4 ⋅ 1 3 ⋅ e - 4 t

v 0 = 10 ⋅ e - 4 t   V ,     t > 0

Por fim, temos que nossa tensão v x será dada por

v x = 1 3 + 1 ⋅ v l = 2 . 5 ⋅ e - t   V ,     t > 0

Resposta

v 0 = 10 ⋅ e - 4 t   V ,     v x = 2 . 5 ⋅ e - t   V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A questão quer a porcentagem de energia inicial armazenada que será dissipada pelo resistor de 60Ω . Simbora!
Na questão já se tem as equações de tensão e corrente, então a partir delas, deduzir algumas informações dos circuitos, bora resolver?
Depois de a chave no circuito da Figura P7.35 estar aberta por um longo tempo, ela é fechada em t = 0. Calcule (a) o valor inicial de i; (b) o valor final de i; (c) a constante de tempo para t ≥ 0 . (
A chave do circuito mostrado na Figura P7.36 esteve na posição a por um longo tempo antes de passar para a posição b em t = 0. a) Determine as expressões numéricas para i L(t) e vo (t) quando t $ 0. b
A chave do circuito mostrado na Figura P7.37 esteve na posição a por um longo tempo. Em t = 0, ela passa instantaneamente para a posição b. a) Determine a expressão numérica para i o (t) quando t $ 0.