Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 40
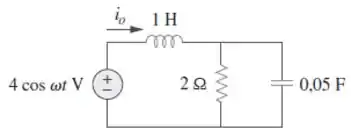
No circuito da Figura , determine quando:
- ;
- ;
- .
Passo 1
Pessoal, a primeira coisa que devemos fazer é encontrar a impedância equivalente do circuito. Vamos para a letra (a). Passando os elementos do circuito para o domínio da frequência, temos:
De início vamos calcular o equivalente paralelo .
Uma vez que achamos, vamos achar o
A corrente pode ser calculada através da divisão da tensão pela impedância total:
No domínio do tempo:
Passo 2
Vamos para a letra (b). Passando os elementos do circuito para o domínio da frequência, temos:
De início vamos calcular o equivalente paralelo .
Uma vez que achamos, vamos achar o
A corrente pode ser calculada através da divisão da tensão pela impedância total:
No domínio do tempo:
Passo 3
Por fim, vamos para a letra (c). Passando os elementos do circuito para o domínio da frequência, temos:
De início vamos calcular o equivalente paralelo .
Uma vez que achamos, vamos achar o
A corrente pode ser calculada através da divisão da tensão pela impedância total:
No domínio do tempo:
Resposta
- ;
- .