Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 38

Usando a figura 9.45 , elabore um problema para ajudar outros estudantes a entender melhor a admitância.

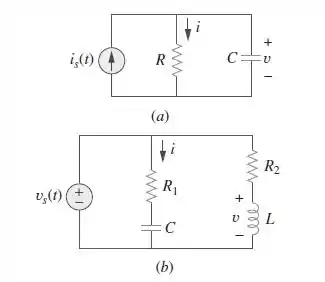
Passo 1

Pessoal, vamos resolver as seguintes questões:

“(a) calcular v e i para o circuito letra a ;

(b) Calcular v e i para o circuito letra b .”

Bora lá! A admitância pode ser encontrada através do inverso da impedância. Portanto, no nosso circuito letra (a) vamos calcular a admitância dos componentes:

Y R = 1 R

Y C = 1 X C = 1 1 j ω C = j ω C

Quando temos admitâncias conectadas em paralelo, que é o nosso caso, a admitância equivalente é obtida pela soma das admitâncias individuais. Portanto,

Y t o t a l = Y R + Y C

Y t o t a l = 1 R + j ω C

A tensão em cima do resistor é a mesma no capacitor, já que R   é paralelo a C .

v = i s Y t o t a l

v = i s 1 R + j ω C

v = i s R 1 + j ω C

Passo 2

Uma vez que encontramos a tensão, podemos achar a corrente que passa no resistor!

i = v × Y R

Substituindo os valores:

i = i s R 1 + j ω R C × 1 R

i = i s 1 + j ω R C

Passo 3

Agora na letra (b), o primeiro passo que devemos fazer é encontrar as impedâncias equivalentes em cada ramo:

  • R 1 está conectado em série com C : Z R 1 C = R 1 + 1 j ω C
  • R 2 está conectado em série com L : Z R 2 L = R 2 + j ω L

Assim, a corrente que passa por Z R 1 C é:

i = V S Z R 1 C

i = V s × Y R 1 C

i = V S R 1 + 1 j ω C

i = j ω C V s 1 + j ω R 1 C

Para encontrarmos v , vamos aplicar um divisor de tensão:

v = j ω L R 2 + j ω L × V s

v = V S j ω L R 2 + j ω L

Resposta

  1. v = i s R 1 + j ω C e i = i s 1 + j ω R C
  2. v = V S j ω L R 2 + j ω L e i = j ω C V s 1 + j ω R 1 C
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um circuito de áudio em série é apresentado na Figura 9.88.Qual é a impedância?Se a frequência for dividida pela metade, qual seria a impedância do circuito?
O circuito da Figura 9.87 faz parte do esquema que descreve um sensor eletrônico industrial. Qual é a impedância total do circuito em 2k H z ?
Uma carga industrial cujo modelo é uma associação em série de uma capacitância e uma resistência é mostrada na Figura 9.89. Calcule o valor de um capacitor C na associação em série de modo que a imped
Uma bobina industrial é representada por um modelo que é uma associação em série de uma indutância L e uma resistência R , conforme mostrado na Figura 9.90. Uma vez que um voltímetro CA mede apenas a
Uma linha de transmissão tem uma impedância em série igual a Z=100 ∠ 75 ° Ω e uma admitância shunt de Y=450 ∠ 48 °μ S . Determine: (a) a impedância característica Z o = Z / Y (b) a constante de propag