Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 59
59- Para o circuito da Figura , determine . Considere
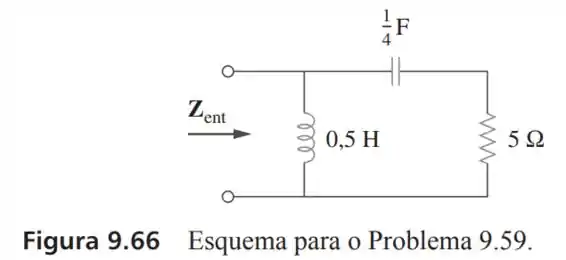
Passo 1
A reatância do indutor e do capacitor nesse circuito serão de:
Passo 2
E a impedância resultante será a reatância de em paralelo com a impedância de o que nos dá:
Transformando os dois números complexos em fasor nós teremos:
Resposta
Exercícios de Livros Relacionados
Determine a admitância Y a b no circuito visto na Figura P9.23. Expresse Y a b em forma polar e também em forma retangular. Determine o valor de Y a b em milissiemens.
a) Mostre que, a uma dada frequência ω , os circuitos na Figura P9.20(a) e (b) terão a mesma impedância entre os terminais a,b se R 1 = R 2 1 + ω 2 R 2 2 C 2 2 C 1 = 1 + ω 2 R 2 2 C 2 2 ω 2 R 2 2 C 2
a) Usando os valores dos componentes do apêndice H, determine um único capacitor ou uma rede de capacitores que, quando combinados em paralelo com o circuito RL do Problema 9.26(a), resulta em uma imp
a) Para o circuito mostrado na Figura P9.24, determine a frequência (em radianos por segundo) em que a impedância Z a b é puramente resistiva. b) Determine o valor de Z a b na frequência determinada n
Determine a impedância Z a b no circuito da Figura P9.22. Expresse Z a b em forma polar e também em forma retangular.