Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 10
Determine no circuito da Figura 13.78.
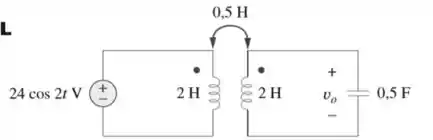
Passo 1
Essa questão exige um pouquinho de atenção a mais, mas não se procupem! Primeiramente temos que nos atentar para a posição dos enrolamentos nas bobinas. Considere o circuito abaixo, considerando as simplificações dos indudores e do capacitor:
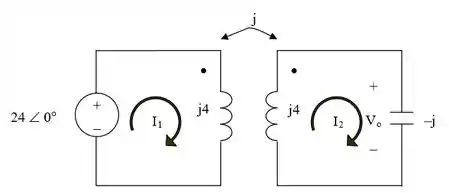
Passo 2
Fazendo uma rapidinha analise das malhas, temo que para a malha 1:
Na forma da matriz:
Passo 3
Resolvendo isso para acharmos a corrente e a tensão, temos que:
Resposta
Exercícios de Livros Relacionados
Use a análise de malhas para determinar i x na Figura 13.80, onde i s = 4c o s ( 600 t ) Aev s = 110c o s ( 600 t+30 ° )
Determine a indutância equivalente, L e q , no circuito da Figura 13.81.
Considere o circuito da Figura 13.82 e determine a impedância vista pela fonte.
Obtenha o circuito equivalente de Thévenin para o circuito da Figura 13.83 nos terminais a-b.
Determine o equivalente de Norton para o circuito da Figura 13.84 nos terminais a-b.