Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 5.Problemas - Ex. 42
O circuito no interior da área sombreada da Figura P5.42 é uma fonte de corrente constante para uma faixa limitada de valores de .
a) Determine o valor de para .
b) Determine o valor máximo de RL para o qual tenha o valor definido em (a).
c) Suponha que Explique o funcionamento do circuito. Você pode admitir que sob todas as condições de operação.
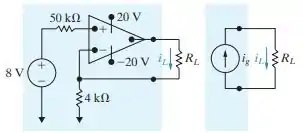
d) Desenhe um gráfico de versus para .
Passo 1
Falaiii meus xuxu’s, ceis tão bonzinho??
Espero que sim hein, bora lá pra mais uma?
Encostaaaa
Redesenhando o circuito como mostrada abaixo
Passo 2
- Para um amplificador operacional ideal
- Do circuito, a tensão de saída é
- Quando o amp-op está operando em região linear, a corrente de carga é independente de . Da parte (b), o amp-op opera em região linear, quando . Portanto, quando , o amp-op está saturado.
- Da parte (b) o amp op opera em região linear para e opera em saturação, quando .
Do circuito
Suponhamos que o amplificador operacional esteja operado dentro de sua faixa linear, então a correte de carga é
Para , a tensão de saída é
Desde a saída . A suposição de operação linear está correta.
Portanto, a corrente de carga é 2mA.
Passo 3
O valor máxima de é 20V. Agora, calcule o valor máximo de PARA é
Portanto, o valor máximo de resistência de carga é de
Passo 4
Se o amplificador operacional estiver saturado, a tensão de saída é igual à sua tensão de alimentação.
Como , a corrente de carga é
Quando, , o amp – op está saturado e a tensão de saída é e a corrente de carga é .
Passo 5
Quando op-amp está na região linear , a corrente de carga é
Quando op-amp está na região de saturação , acorrente de carga é
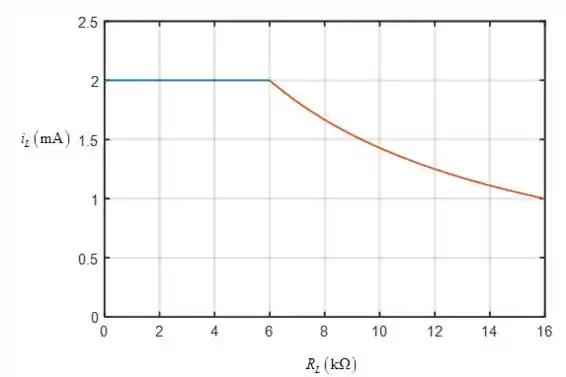
O esboço versus é mostrado abaixo
Resposta
- Portanto, a corrente de carga é 2mA.
- Portanto, o valor máximo de resistência de carga é de .
- Quando, , o amp – op está saturado e a tensão de saída é e a corrente de carga é .
- Vide o passo 5.