Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 12.Problemas - Ex. 29
Um sistema trifásico estrela-triângulo equilibrado possui e. Se a impedância de linha por fase for , determine a potência complexa total para a carga.
Passo 1
Questão bem de boas pessoal, atenção hein! Primeiro, podemos substituir a carga em delta por uma carga em estrela. No caso,
O equivalente monofásico do circuito é mostrado desse jeito:
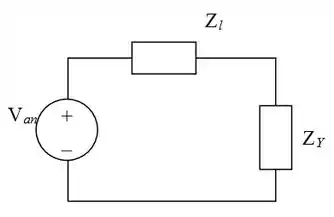
Passo 2
Portanto, a partir do circuito simples, podemos calcular a potencia!
Portanto a potência é igual a:
Resposta
Exercícios de Livros Relacionados
Uma fonte equilibrada conectada em Y , com V a n = 200 ∠ 0 ∘ V (eficazes), de sequência positiva, é conectada por meio de quatro condutores perfeitos (com impedância igual a zero) a uma carga desbalan
Uma carga trifásica equilibrada conectada em Y consome 3 k W , com fator de potência 0,8 atrasado. Um Y equilibrado de capacitores é colocado em paralelo com a carga, de forma que o fator de potência
Na Fig. 13.10, a fonte e equilibrada, com sequência de fase positiva, e V e = = 1000V V (eficazes). Calcule Z p , se a fonte entrega 3,6k W com fator de poténcia 0,6 adiantado
Se o fio neutro for removido do sistema do Prob. 13.9, calcule as correntes de linha.
Um sistema equilibrado em Y-Y, trifásico e de sequência de fases positiva, tem V a n = 200 / 0 ∘ V (eficazes) e Z p = 3 + j 4 Ω . As linhas têm uma resistência de 1 Ω cada uma. Calcule a corrente de l