Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 12.Problemas - Ex. 35

Três impedâncias iguais, de 60 + j30 Ω cada, são ligadas em triângulo a um circuito trifásico de 230 V RMS. Outras três impedâncias iguais, de 40 + j10 Ω cada, são ligadas em estrela no mesmo circuito e nos mesmos pontos. Determine

(a) A corrente de linha.

(b) A potência complexa total fornecida para as duas cargas.

(c) O fator de potência das duas cargas associadas.

Passo 1

Primeiro passo quando se depara com questões onde uma das cargas está ligado em triângulo e a outra em estrela é transformá-la todas em estrela, desse modo podemos fazer o circuito monofásico equivalente.

Assim, a carga conectada em delta é convertida em seu equivalente conectado em estrela:

Z Y ' ' = 1 3 Z Δ

Z Y ' ' = 60 + j 30 3 = 30 + j 10   Ω

Desse modo, o circuito monofásico equivalente é dado por:

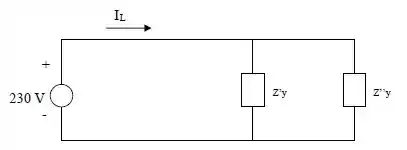
Passo 2

Certo! Agora ficou mais fácil calcular a corrente de linha, basta fazermos o paralelo entre as impedâncias, e aplicar a relação entre impedância e tensão.

Com isso, temos:

Z   y = Z ' y   / /   Z   ' '   y   = ( 40 +   j 10 )   / / ( 20 +   j 10 )  

Z Y = 13.5 + j 5.5   Ω

Logo,

I L = V L Z Y

I L = 230 13.5 + j 5.5

I L = 14.61 - j 5.953   A

Passo 3

Certo! Agora vamos encontrar a potência complexa. Lembre-se que:

S = 3 * V L * I L *

S = 3 * 230 * [ 14.61 - j 5.953 ]

S = 10.081 + j 4.108   k V A

Passo 4

Para o cálculo do fator de potência podemos olhar para a impedância equivalente. Note que:

Z Y = 13.5 + j 5.5   Ω

Z Y = 14.58 ∠ 22.17 °

Logo,

F P = cos ⁡ 22.17

F P = 0.9261  

Resposta

a )   I L = 14.61 - j 5.953   A

b )   S = 10.081 + j 4.108   k V A

c )   F P = 0.9261  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma fonte trifásica equilibrada, de sequência positiva, com V a b = 240 ∠ 0 °V (eficazes), está alimentando uma combinação em paralelo de uma carga conectada em Y com uma outra carga em Δ . Se as carg
Uma fonte trifásica equilibrada, de sequência positiva, com V a b = 240 ∠ 0 °V (eficazes), entrega 43.2k W , com fator de potência unitário, a uma combinação em paralelo de uma carga conectada em Y co
Para um sistema trifásico equilibrado, se as tensões de fase são v a ( t ) = V m cos ⁡ ( ω t ) v b ( t ) = V m cos ⁡ ( ω t - 120 ° ) v c ( t ) = V m cos ⁡ ( ω t - 240 ° ) Então as correntes de fase sã
Demonstre (13.24).
No sistema da Fig. 13.20, as tensões de linha são um conjunto equilibrado, de sequência positiva, com V a b = 200 ∠ 0 °V (eficazes) e Z 1 = Z 2 = Z 3 = 10 ∠ 30 °Ω . Calcule a potência entregue à carga