Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 12.Problemas - Ex. 34
Uma carga conectada em estrela equilibrada com impedância por fase de 10 – j16 é conectada a um gerador trifásico equilibrado com tensão de linha 220 V. Determine a corrente de linha e a potência complexa absorvida pela carga.
Passo 1
Primeiro passo quando se depara com questões de trifásico é imaginar o circuito. Desse modo,
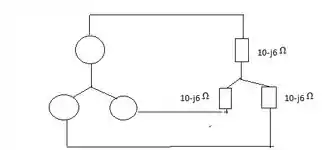
Passo 2
Note que, como a tensão é de linha, e as cargas são por fase, devemos fase a transformação da tensão de linha para tensão de fase, desse modo:
Assim, já podemos usar a lei de Ohm. Com isso a corrente é dada por:
Portanto, como a corrente de linha é somente o modulo, temos que:
Passo 3
Certo! Agora vamos encontrar a potência complexa. Lembre-se que:
Resposta
Exercícios de Livros Relacionados
Para o sistema mostrado abaixo, as tensões de linha são um conjunto equilibrado de sequência positiva com V a b = 300 ∠ 0 °V (eficazes). Calcule a leitura dos medidores P A e P B e a potência total en
Mostre que, se uma fonte equilibrada, de sequência positiva, é conectada por meio de três fios perfeitamente condutores a uma carga equilibrada tenho impedâncias de fase Z p = Z p ∠ 0 ° , então os doi
Encontre as leituras dos wattímetros, conectados como no Prob. 13.34, para o sistema do Prob 13.23.
Repita o Prob. 13.38 para o sistema do Prob. 13.27.
Repita o Prob. 13.4 . 1 para o sistema do Prob.