Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 7.Problemas - Ex. 29

As indutâncias mostradas são todas em mH. Calcule a indutância equivalente vista pelos terminais a e b:

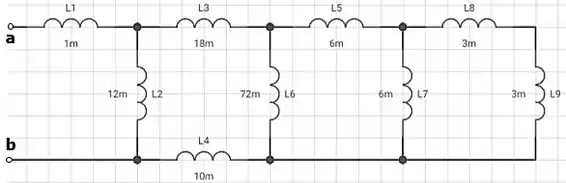
Passo 1

Tudo bem galerinha?! Essa questão com certeza precisa de toda nossa atenção, então vamos manter o foco e resolvê-la bem devagar…

Nossa análise começará da direita para a esquerda, onde temos L 8 e série com L 9 . Para quem tiver esquecido como se calcula a indutância para as ligações em série e em paralelo, vamos anotar aqui em baixo:

Sendo assim, teremos:

L 89 = L 8 + L 9 =   3 + 3 =   6   m H

Assim podemos desenhar o circuito como:

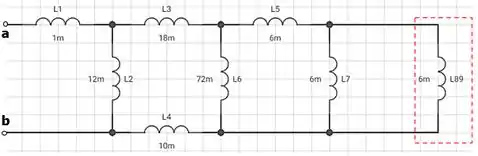
Passo 2

Nesta nova configuração, temos L 8 9 em paralelo com L 7 , então vamos calcular L 7 89 :

L 789 = L 89 ∙ L 7 L 89 + L 7 =   6 ∙ 6 6 + 6 =   3   m H

Isso nos permite reduzir o circuito para:

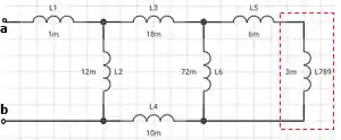
Até esse passo, tudo correu bem 😊, então vamos seguir…

Passo 3

Agora temos L 5 em série com L 7 89 , então vamos calcular L 5 789 :

L 5789 =   L 789 +   L 5 =   3 + 6 = 9   m H

Assim teremos:

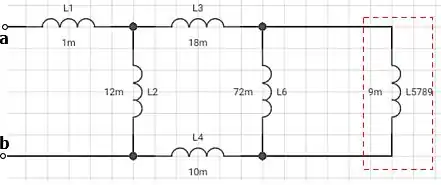
Passo 4

Agora temos L 6 em paralelo com L 5 789 , então vamos calcular L 5 6 789 :

L 56 789 = L 5789 ∙ L 6 L 5789 + L 6 =   72 ∙ 9 72 + 9 =   8   m H

Desta forma, podemos reescrever o circuito como:

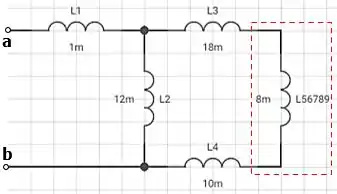
O circuito já está ficando com um aspecto mais simples 😉

Passo 5

Percebam, que agora, L 56789 , L 4 e L 3 estão em série, isso torna nosso cálculo mais simples, então temos:

L 43 56789 =   L 56789   + L 4 + L 3 =   10 + 8 + 18 =   36   m H

Isso reduzi nosso circuito ainda mais:

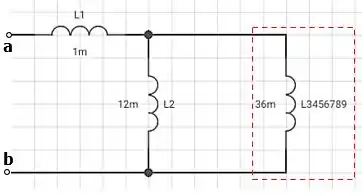
Passo 6

Assim temos, L 34 56789 em paralelo com L 2 , logo:

L 234 56789 = L 34 5789 ∙ L 2 L 34 5789 + L 2 =   36 ∙ 12 36 + 12 =   9   m H

O nos deixa com um circuito ainda menor:

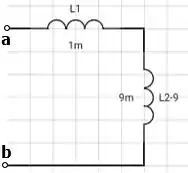
Passo 7

Desta forma, nos restou apenas dois indutores em série, sendo a L e q expressa por:

L e q =   L 2 - 9   + L 1 =   9 + 1 =   10   m H

Resposta

A indutância equivalente do circuito, corresponde a 10 mH.

Exercícios de Livros Relacionados

A tensão nos terminais do indutor de 750 mH da Figura P6.7(a) é mostrada na Figura P6.7(b). Sabe-se que a corrente i do indutor é igual a zero para t ≤0 . a) Escreva as expressões para i em t ≥ 0 . b)
Avalie a integral ∫ 0 ∞ pd t para o Exemplo 6.2. Comente o significado do resultado.
Sabe-se que a corrente em um indutor de 50m Hé é i=120m A ,t ≤0 ; i=A 1 e - 500 t+A 2 e - 2.000 tA ,t ≥0 A tensão no indutor (convenção passiva) é 3 V em t = 0. a) Determine a expressão para a tensão
Sabe-se que a corrente em um indutor de 150 mH é i L=25 t e - 500 tAp a r at≥ 0 Determine a tensão no indutor para t0 (Suponha a convenção passiva)Determine a potência (em microwatts) nos terminais do
O pulso triangular de corrente mostrado na Figura P6.2 é aplicado a um indutor de 500 mH. a) Escreva as expressões que descrevem i(t) nos quatro i n t e r v a l o st,0 ,0 ≤t-25m s ,25m s ≤t ≤50m set.5