Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 32
32. Determine e no circuito da figura usando a análise de malhas.
Passo 1
Fala galerinha! Vamos pra mais um problema sobre circuitos com corrente alternada.
Olha só! Todos os elementos do nosso circuito já estão na forma fasorial.
Bom pra gente, né não! Bora partir logo pra análise de malhas!
Passo 2
Nesse passo, vamos preparar o circuito pra utilizar a nossa análise de malhas. Quando digo preparar, é simplesmente nomear as correntes de malha!
E aqui está nossa bela figura:
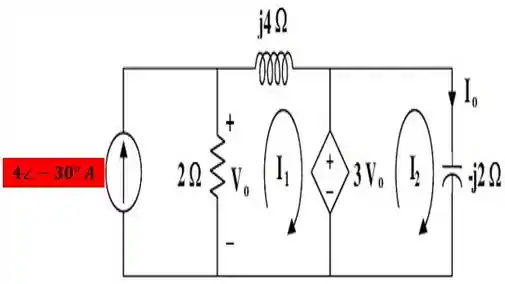
Você deve estar se perguntando!? Por que aquela malha mais a esquerda não tem corrente de malha nomeada?
A resposta é simples. Ela já tem uma corrente de malha e vale .
Desse modo... Aplicando a lei das tensões de para a malha , obtemos que:
Só que a tensão , como podemos ver no circuito, é dada por:
Desse modo, a nossa equação para a malha vai ficar assim:
E o valor de é dado por:
Passo 3
A corrente presente no circuito, é na verdade, a corrente de malha .
E essa corrente ao passar pelo capacitor de ; gera uma diferença de potencial igual a , como podemos ver na figura do enunciado. Desse modo...
Como já obtemos o valor de ...
Missão cumprida! Resposta encontrada!