Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 14.Problemas - Ex. 44

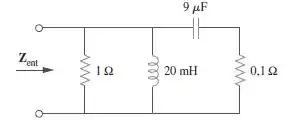
Calcule o circuito da Figura 14.83 e determine:

  1. A frequência de ressonância ω 0
  2. Z e n t ( ω 0 )

Passo 1

Vamos para letra (a), galera! A frequência de ressonância ω 0 para um circuito R L C é a frequência em que a impedância (admitância) do circuito se torna puramente resistiva (condutiva). Assim, para a gente encontrar ω 0 , precisamos encontrar a admitância do circuito e igualar a parte imaginária a zero.

Y e n t = 1 j ω L + 1 R 1 + 1 R 2 + 1 j ω C

Y e n t = 1 R 1 - j ω L + j ω C j ω C R 2 + 1

Vamos multiplicar a fração, o numerador e o denominador, pelo conjugado, temos:

Y e n t = 1 R 1 - j ω L + j ω C + ω 2 C 2 R 2 1 + ω 2 R 2 2 C 2

Y e n t = 1 R 1 + j - 1 ω L + ω C 1 + ω 2 R 2 2 C 2

Passo 2

Vamos agora igualar a zero a parte imaginária da admitância:

- 1 ω L + ω C 1 + ω 2 R 2 2 C 2 = 0

1 ω L = ω C 1 + ω 2 R 2 2 C 2

ω 2 L C 1 + ω 2 R 2 2 C 2 = 1

ω 2 L C = 1 + ω 2 R 2 2 C 2

ω 2 L C - ω 2 R 2 2 C 2 = 1

ω 2 L C - R 2 2 C 2 = 1

ω 2 = 1 L C - R 2 2 C 2

ω = 1 L C - R 2 2 C 2

Substituindo os valores, temos:

ω = 1 0,02 9 × 10 - 6 - 0,1 2 9 × 10 - 6 2

ω = 2357,028   r a d / s

Passo 3

Agora, para a letra (b), queremos achar a impedância Z e n t . Sabemos que:

Z e n t = 1 Y e n t

Assim,

Y e n t = 1 j ω L + 1 R 1 + 1 R 2 + 1 j ω C

Y e n t = 1 1 + 1 j 2357,028 0,02 + 1 0,1 + 1 j 2357,028 9 × 10 - 6

Y e n t ≈ 1   S

Desse modo, a impedância de entrada é igual a:

Z e n t = 1 Y e n t = 1 1 = 1   Ω

Resposta

  1. ω 0 = 2357,028   r a d / s
  2. Z e n t = 1   Ω
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As duas chaves no circuito da Figura P13.35 funcionam simultaneamente. Não há nenhuma energia armazenada no circuito no instante em que elas se fecham. Determine i(t), para t ≥ 0+, a partir do equival
A chave no circuito da Figura P13.28 esteve na posição a por um longo tempo. Em t = 0, ela passa instantaneamente para a posição b. a) Determine Vo. b) Determine vo.
Começando com a Equação 13.65, mostre que a corrente no capacitor do circuito da Figura 13.19 é positiva para 0 μs e negativa para t200 μ s. Mostre também que em 200 μ s a corrente é nula e que isso c
A chave no circuito da Figura P13.29 esteve na posição a por um longo tempo antes de passar instantaneamente para a posição b, em t = 0. a) Construa o circuito equivalente no domínio da frequência, pa
No circuito da Figura P13.41, a chave 1 é fechada em t = 0 e a chave do tipo liga-antes-interrompe-depois passa instantaneamente da posição a para a posição b. a) Construa o circuito equivalente no do