Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 31
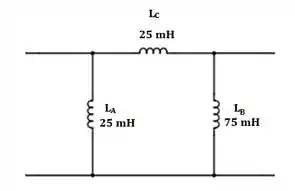
Considere a Figura e elabora um problema para ajudar outros estudantes a entender melhor os transformadores lineares e como determinar os circuitos equivalente e equivalente
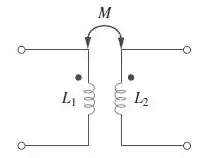
Passo 1
Galera, vamos resolver a seguinte questão:
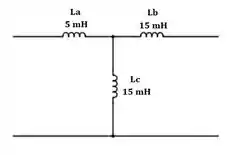
“Obtenha os circuitos equivalentes e pi do transformador linear mostrado na figura quando , e ”.
Para o equivalente , precisamos achar os parâmetros do circuito. Logo,
Assim, o circuito equivalente é:
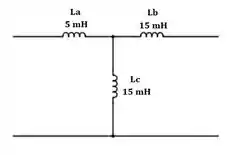
Passo 2
Agora, para montarmos o equivalente pi, precisamos calcular os componentes dele, que são um pouco diferentes do :
Assim, o circuito equivalente pi é:
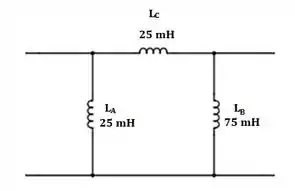
Resposta
O equivalente é:
O equivalente pi é:
Exercícios de Livros Relacionados
Dois transformadores lineares são colocados em cascata, conforme mostrado na Figura 13.101 . Demonstre que Z e n t = ω 2 R L a 2 + L a L b - M a 2 + j ω 3 L a 2 L b + L a L b 2 - L a M b 2 - L b M a 2
No circuito da Figura 13.9 8 , determine o valor do coeficiente de acoplamento k que fará que o resistor de 10Ω dissipe 320W . Para esse valor de k , determine a energia armazenada nas bobinas acoplad
Determine a impedância de entrada do circuito da figura 13.99 usando o conceito de impedância refletidaObtenha a impedância de entrada substituindo o transformador linear por seu circuito equivalente
34. Elabore um problema para ajudar outros estudantes a entender melhor como determinar a impedância de entrada de circuitos com transformadores usando a figura 13.103