Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 34

34. Elabore um problema para ajudar outros estudantes a entender melhor como determinar a impedância de entrada de circuitos com transformadores usando a figura

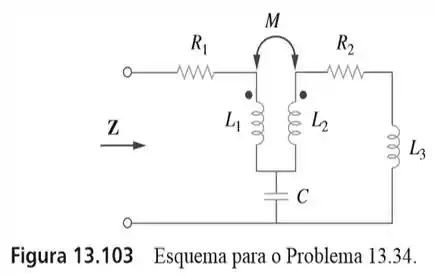
Passo 1

Olha só! Como é um problema cuja elaboração é de nossa responsabilidade, bora redesenhar esse circuito, atribuindo valores numéricos a cada um de seus componentes.

E é claro, além de dar valores aos componentes, bora aproveitar a “deixa” e dar nomes aos bois também! Isto é, nomear as correntes de malha desse circuito, que chamaremos de e , respectivamente.

Aqui está nossa bela imagem:

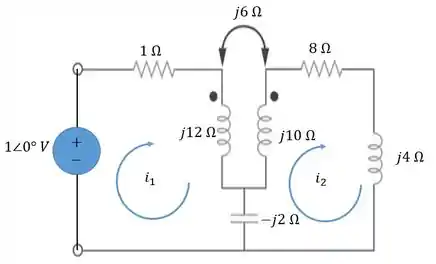
Substituimos a impedância por uma fonte de tensão de . Depois que terminarmos a análise de malhas; para obter , basta dividir a fonte de tensão pela corrente circulando na fonte, no caso .

Passo 2

Bora então, partir pra análise de malhas.

Primeiro, bora aplicar a para a malha :

E depois, bora aplicar a para a malha :

Passo 3

Substituindo em , temos que:

E a outra corrente de malha, , é dada por:

Passo 4

Já a impedância , é dada pelo inverso da corrente . Presta antenção, que só é o inverso porque a fonte de tensão é de . Na prática, o que estamos fazendo é dividir a fonte de tensão pela corrente que nela está circulando.