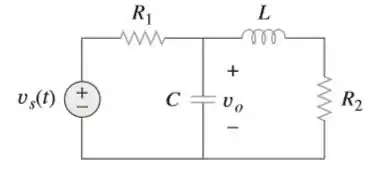
Considere a figura e elabore um problema para ajudar outros estudantes a entender melhor como usar o teorema de Thévenin (no domínio s) para ajudar na análise de circuito.
Passo 1
Vamos desenhar esse circuito no domínio Laplace:
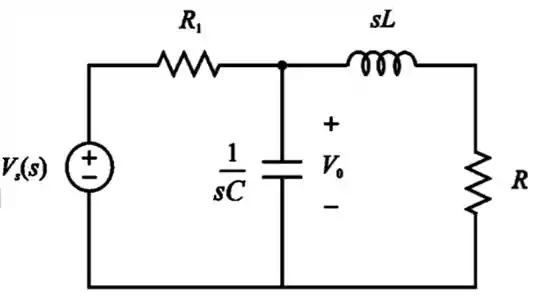
Passo 2
Temos
Passo 3
Vamos então calcular a impedância de Thévenin:
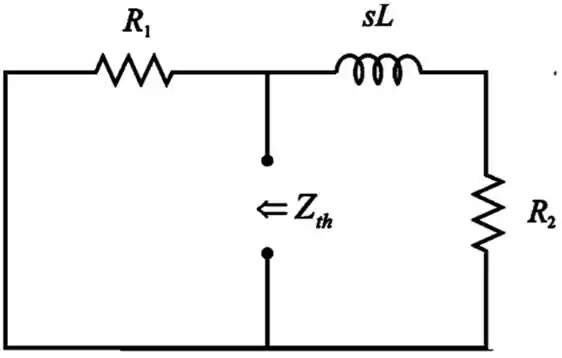
Passo 4
Temos então e em série, e esses dois em paralelo com :
Passo 5
Então, agora vamos querer calcular a tensão de Thévenin.
Vamos antes olhar esse circuito:
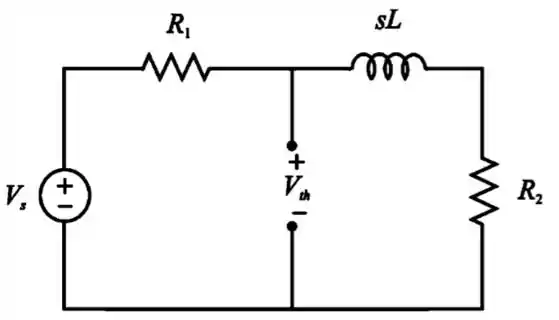
Passo 6
Agora, conseguimos aplicar a análise nodal para achar a tensão de Thévenin:
Passo 7
Então, chegamos no nosso equivalente Thévenin
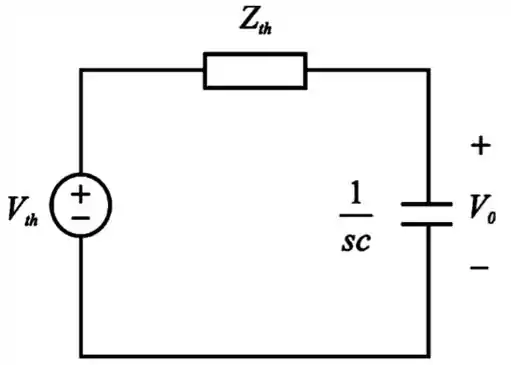
Usando divisor de tensão conseguiremos achar a tensão que passa em cima do capacitor
A partir daí, assuma valores e substitua-os na expressão, e então resolva por expansão em frações parciais. Depois calcula a transformada de Laplace Inversa e então teremos no domínio do tempo.