Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 2.Problemas - Ex. 21

A corrente no circuito mostrado na Figura P2.21 é . Determine (a) ; (b) e (c) a potência fornecida pela fonte de corrente independente.

Passo 1

Iae, meus queridos! Td certinho??

A ideia por traz dessa questão é bem simples, aplicando o método de divisão de correntes, é possível encontrar e logo depois encontrar pelo mesmo método.

Porém vamos resolver de outra forma para exemplificar o leque de possibilidades de resolver um circuito.

O enunciado nos deu , com essa informação, podemos calcular a tensão em todos os 3 resistores em que flui essa corrente, a soma dessas tensões será a tensão no resistor de .

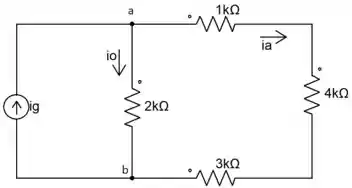
Passo 2

Na letra a), a partir dessa informação, podemos aplicar a lei de ohm e calcular

Na letra b), basta fazermos uma análise no nó a entre as correntes de entradas e saídas, logo

Por fim, na letra c), usamos a equação de potência dada por

É isso! O que achou? Responde Aí 😉👍

Resposta

(a)

(b)

(c)

Exercícios de Livros Relacionados

As correntes i 1 e i 2 no circuito da Figura P2.27 são 21 A e 14 A, respectivamente. a) Determine a potência fornecida por cada fonte de tensão.b) Mostre que a potência total fornecida é igual à potên

Para o circuito mostrado na Figura P2.32, determine v 0 e a potência total fornecida no circuito.

A tabela da Figura P2.31(a) mostra a relação entre a tensão e a corrente nos terminais da fonte real de tensão constante representada na Figura P2.31(b).a) Faça um gráfico de v s versus i s .b) Constr

A tabela da Figura P2.30(a) mostra a relação entre a tensão e a corrente nos terminais da fonte real de corrente constante representada na Figura P2.30(b).a) Faça um gráfico de i s versus v s .b) Cons

Deduza a Equação 2.25. Sugestão: use as equações (3) e (4) do Exemplo 2.11 para expressar i E como uma função de i B. Resolva a Equação (2) para i 2 e substitua o resultado nas equações (5) e (6). Res