Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 2.Problemas - Ex. 30

A tabela da Figura P2.30(a) mostra a relação entre a tensão e a corrente nos terminais da fonte real de corrente constante representada na Figura P2.30(b).

a) Faça um gráfico de i s versus v s .

b) Construa um modelo de circuito dessa fonte de corrente que seja válido para 0 ≤ v s ≤ 75 V , com base na equação da reta representada no gráfico em (a).

c) Use seu modelo de circuito para prever a corrente fornecida a um resistor de 2,5   k V .

d) Use seu modelo de circuito para prever a tensão de circuito aberto da fonte de corrente.

e) Qual é a tensão de circuito aberto real?

f) Explique por que as respostas para (d) e (e) não são iguais.

Passo 1

Iae, meus queridos! Td certinho??

Temos muitas coisas para fazer nessa questão, então bora começar 😉

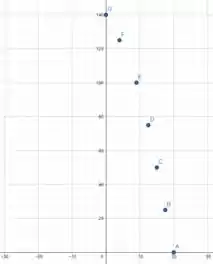
Na letra a), vamos plotar os pontos que foram dados na tabela.

Na letra b), vamos ligar os pontos da reta entre v t = 0 V e v t = 75 V .

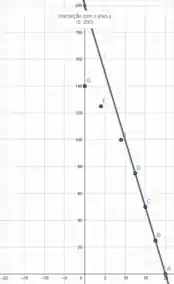
Neste modelo a fonte de tensão associada é de 200 V , como podemos ver no gráfico

Para calcular a resistência associada, vamos usar

R = d v d i

Com valores tabelados entre v t = 0 V e v t = 75 V .

R = 25 - 0 17,5 m - 20 m

R = 10 k Ω .

Para calcular i g , aplicamos a lei de ohm utilizando

i g = v g R → i g = 200 10 k → i g = 20 m A .

Ou vemos na tabela que i g será a corrente i t quando v t = 0 V .

Passo 2

Na letra c) temos o seguinte circuito

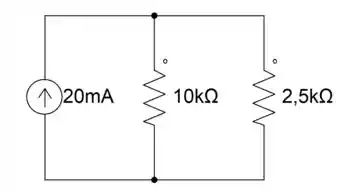
Aplicando o método de divisão de correntes, encontramos i R e aplicamos na formula de potência.

i R = 20 m · 10 k 2,5 k + 10 k

i R = 16 A .

Suapotência será

p = i R 2 · R → p = 640 k W .

Na letra d) o valor da tensão com o circuito aberto, será igual o valor da fonte de tenção associada, ou seja, 200V.

Na letra e) vemos que pela tabela, quando i t = 0 A , v t = 140 V , logo, essa é a tensão de circuito aberto.

Por fim, na letra f), podemos explicar que por se tratar de uma fonte real de corrente, essa diferença ocorre, pois, fontes reais possuem perdas que podem fazer com que seus valores se distanciam um pouco de uma fonte ideal.

É isso! O que achou? Responde Aí 😉👍

Resposta

(a) gráfico no passo-a-passo.

(b) uma fonte de corrente de 20 A em paralelo com um resistor de 10 k Ω .,

(c) p = 640 k W .

(d) 200V.

(e) 140V.

(f) explicação no passo-a-passo.

Exercícios de Livros Relacionados

No gráfico do circuito do Problema 4.8, selecione a arvore das fontes de tensão e o resistor de 12 Ω . Empregando o método desta seção, escreva uma equação da LKC e caIcule v.
Considere o circuito mostrado na Figura P2.17. a) Determine v 0 usando as leis de Kirchhoff e a lei de Ohm. b) Teste a solução para v 0 , verificando que a potência total fornecida é igual à potência
a) Determine as correntes i 1 e i 2 no circuito da Figura P2.19. b) Determine a tensão v 0 . c) Verifique que a potência total fornecida é igual à potência total consumida.
A corrente i x no circuito mostrado na Figura P2.20 é 50 mA e a tensão v x é 3,5 V. Determine (a) i 1 ; (b) v 1 ; (c) v g ; e (d) a potência fornecida pela fonte de corrente.
Dado o circuito mostrado na Figura P2.18, determine a) o valor de i a , b) o valor de i b , c) o valor de v 0 , d) a potência dissipada em cada resistor, e) a potência fornecida pela fonte de 50 V.