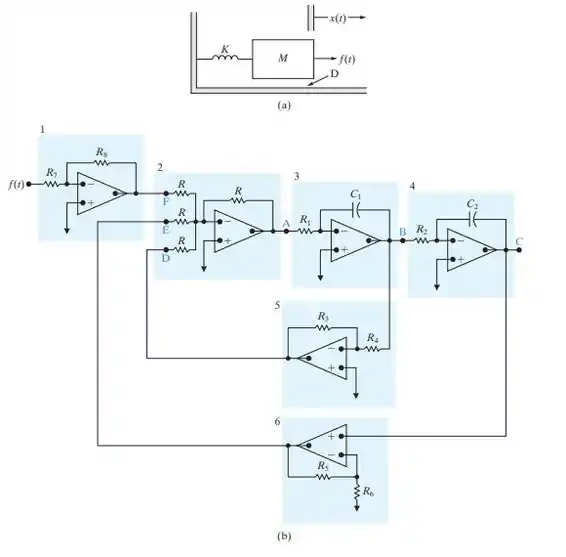
Agora, queremos ilustrar como vários circuitos amp op podem ser interligados para resolver uma equação diferencial. a) Deduza a equação diferencial para o sistema mola-massa mostrado na Figura P8.65(a). Admita que a força exercida pela mola seja diretamente proporcional ao deslocamento da mola, que a massa é constante e que a força de atrito é diretamente proporcional à velocidade da massa. b) Reescreva a equação diferencial deduzida em (a) de modo que a derivada de ordem mais alta seja expressa como uma função de todos os outros termos da equação. Agora, admita que uma tensão igual a d2x/dt2 esteja disponível e, por integrações sucessivas, gere dx/dt e x. Podemos obter os coeficientes nas equações a partir dos fatores de escala dos amplificadores e combinar os termos necessários para gerar d2x/dt2 usando um amplificador somador. Com essas ideias em mente, analise a interligação mostrada na Figura P8.65(b). Em particular, descreva a função de cada área sombreada no circuito e o sinal nos pontos rotulados B, C, D, E e F, admitindo que o sinal em A represente d2x/dt2. Discuta também os parâmetros R; R1, C1; R2, C2; R3, R4; R5, R6 e R7, R8 em termos dos coeficientes da equação diferencial.

Passo 1

Passo 2

Resposta