Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 67

Dado o circuito com AOP da figura, se v 1 ( 0 + ) = 2 e v 2 ( 0 + ) = 0 V , determine v 0 para t > 0 . Seja R = 100 k Ω e C = 1 μ F .

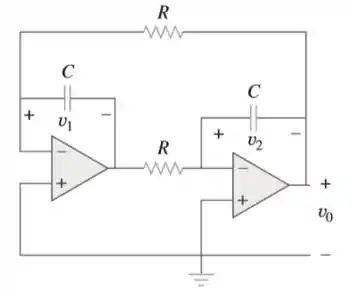
Passo 1

Desenhando o circuito no domínio da frequência e considerando as condições iniciais das tensões que passam nos capacitores ( v 1 ( 0 ) = 2 V e v 2 ( 0 ) = 0 V ):

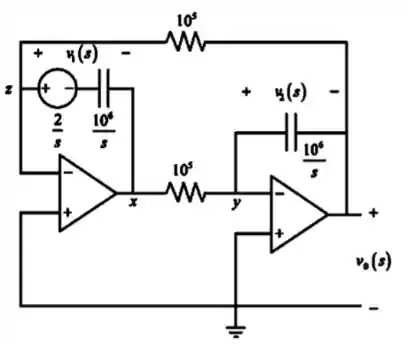
Passo 2

Por ser um amplificador, a corrente entrando nele é zero e as tensões nos nós y e x são iguais a zero já que os terminais positivos dos dois amplificadores estão aterrados:

Utilizando a lei dos nós no nó x , e isolando V x ( s ) , temos:

V x ( s ) - V y ( s ) 1 0 5 + V z ( s ) - [ V z ( s )   -   v 1 ( 0 + ) ] 1 0 6 s = 0

V x ( s ) [ 1 1 0 5 +   s 1 0 6 ] = V y ( s ) [ 1 1 0 5 ] + [ V z ( s ) - v 1 ( 0 + ) ] [ s 1 0 6 ]

Passo 3

Substituindo V y ( s ) e V z ( s ) por zero e substituindo v 1 ( 0 + ) por 2 s :

V x ( s )   = - 2 s + 10

Passo 4

De modo similar, utilizando a lei dos nós no nó y , temos:

V y ( s ) - v o ( s ) 1 0 6 s + V y ( s ) - V x ( s ) 1 0 5 = 0

E substituindo V y ( s ) por zero:

v o ( s ) =   - V x ( s ) [ 10 s ]

Passo 5

Substituindo o V x ( s ) que achamos no Passo 2, teremos:

v o ( s ) = 20 s ( s + 10 )

Passo 6

Separando em frações parciais teremos:

v o ( s ) = 20 s ( s + 10 ) = A s + B s + 10

Agora basta encontrar A ,   B   e   C e encontrar V .

A = 2

B =   - 2

Daí, substituindo, teremos:

Por Laplace utilizando a tabela de transformadas, teremos:

v o ( t )   = 2 [ 1 - e - 10 t ] u ( t )     V , para t>0.

Resposta

v o ( t )   = 2 [ 1 - e - 10 t ] u ( t )     V , para t>0.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A chave no circuito da Figura P13.40 esteve fechada por um longo tempo, antes de abrir em t = 0. Use o método da transformada de Laplace para determinar vo.
Não há nenhuma energia armazenada no circuito apresentado na Figura P13.43 no instante em que as duas fontes são conectadas. a) Use o princípio da superposição para determinar Vo. b) Determine v o , p
Não há nenhuma energia armazenada no circuito da Figura P13.34 no instante em que a fonte de tensão é energizada. a) Determine Vo, Io e IL. b) Determine vo, i o e i L, para t $ 0
A chave do tipo liga-antes-interrompe-depois no circuito da Figura P13.39 esteve na posição a por um longo tempo. Em t = 0, ela passa instantaneamente para a posição b. Determine i o , para t ≥ 0.
Não há nenhuma energia armazenada no circuito da Figura P13.25, no instante em que a chave é fechada. a) Determine v o , para t ≥ 0. b) Sua solução faz sentido em termos do comportamento conhecido do