Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 13.Problemas - Ex. 39

A chave do tipo liga-antes-interrompe-depois no circuito da Figura P13.39 esteve na posição a por um longo tempo. Em t = 0, ela passa instantaneamente para a posição b. Determine i o , para t ≥ 0.

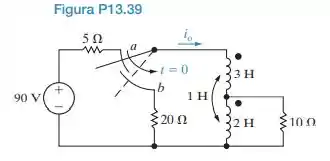
Passo 1

Falaaa, pessoal! Como vocês estão?

Bora pra mais uma questãozinha pra exercitar o que a gente sabe sobre transformada de Laplace na análise de circuitos!

Observando o sistema acima, notamos que para t

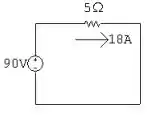
Para t> 0 + :

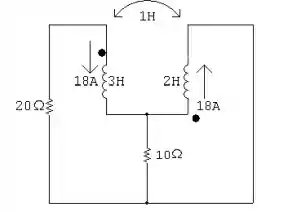
Uma vez que isso esteja fixado, podemos extrair o seguinte sistema de equações:

L 1 - M = 3 + I = 4 H

L 2 - M = 2 + I = 3 H

Passo 2

Esse sistema depois de desenvolvido, nos dá o seguinte sistema mostrado na ilustração:

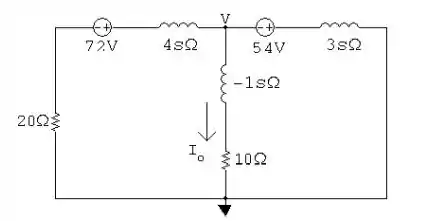
De onde tiramos que:

V - 72 4 s + 20 + V - s + 10 + V + 54 3 s = 0

Isolando V, temos que:

V = 72 3 s - 54 4 s + 20 ( - s + 10 ) 5 s 2 + 110 s + 200

Portanto, teremos:

I 0 = V - s + 10 = - 1,2 s + 2 + 1,2 s + 20

Por fim:

i 0 t = 1,2 e - 20 t - e - 2 t u t A

Resposta

i 0 t = 1,2 e - 20 t - e - 2 t u t A

Exercícios de Livros Relacionados

No circuito da figura, a chave esteve na posição 1 por um longo tempo antes de ser movida para a posição 2 em t = 0 . Determine: v ( 0 + ) ,d v ( 0 + ) d t v ( t ) para t ≥ 0 .
Determine i_o ( t ) para t0 no circuito na figura.
Determine i_0 ( t ) no circuito da figura.
Se a chave na figura esteve fechada a um longo tempo antes de t = 0 , instante no qual é aberta, determine i x e v R para t0 .
Determine V_x ( s ) no circuito da figura.