Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 8
Determine para o circuito da Figura 13.77.
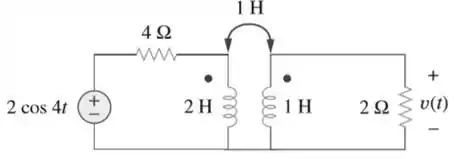
Passo 1
All right! Vamo que vamo! Primeiro vamos transformar esses dois indutores do transformador em impedancias complexas, para facilitar nossa vida posteriormente!
Considere o circuito abaixo:
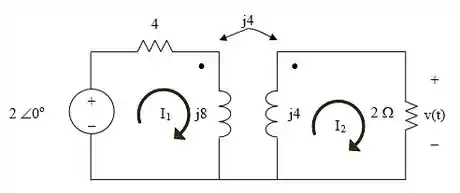
Passo 2
Para ele, vamos fazer uma analise de malhas e tentar achar a corrente para acharmos tensão
Na forma da matriz, essas equações se tornam:
Passo 3
Resolvendo isso, teremos que:
Portanto para finalizar em fim essa questão, teremos que
Resposta
Exercícios de Livros Relacionados
Para as três bobinas acopladas da Figura 13.72, calcule a indutância total.
Considere a figura 13.73 e elabore um problema para ajudar outros estudantes a entender melhor a indutância mútua.
Duas bobinas ligadas de forma a favorecer a conexão em série possuem indutância total de 500m H . Quando ligadas em uma configuração de forma a se opor à conexão em série, as bobinas apresentam uma in
Duas bobinas estão acopladas mutuamente, com L 1=50m H , L 2=120m Hek=0,5 . Calcule a máxima indutância possível se:As duas bobinas estiverem conectadas em sérieAs duas bobibnas estiverem conectadas e
Para as bobinas acopladas na Figura 13.74a, demonstre que L e q = L 1 + L 2 + 2 M Para as bobinas acopladas na Figura 13.74b demonstre que L e q = L 1 L 2 - M 2 L 1 + L 2 - 2 M