Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 47

Determine i_0 ( t ) para t > 0 no circuito da figura.

Passo 1

Achar as condições iniciais (o indutor vira um curto circuito e o capacitor vira um aberto):

Passo 2

A partir daí sabemos que:

i_o ( 0^- ) = 5 A

V_o ( 0^- ) = 0 V

E são essas condições iniciais que iremos incorporar ao nosso circuito no domínio de Laplace abaixo:

Passo 3

Vamos aplicar a lei dos nós ao nó V_o :

(V_o - (15)/(s))/(1) + (V_o)/(2 s) + (5)/(s) + (V_o - 0)/(4 + (4)/(s)) = 0

(15)/(s) - (5)/(s) = (1 + (1)/(2 s) + (s)/(4 ( s + 1 ))) V_o

(10)/(s) = (4 s^2 + 4 s + 2 s + 2 + s^2)/(4 s ( s + 1 )) V_o

(10)/(s) = (5 s^2 + 6 s_ + 2)/(4 s ( s + 1 )) V_o

V_o = (40 ( s + 1 ))/(5 s^2 + 6 s + 2)

I_o = (V_o)/(2 s) + (5)/(s) = (4 ( s + 1 ))/(s ( s^2 + 1.2 s + 0.4 )) + (5)/(s)

Passo 4

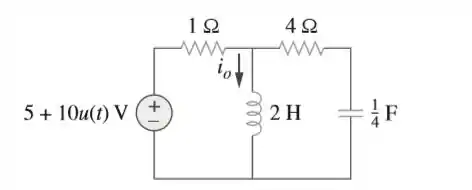
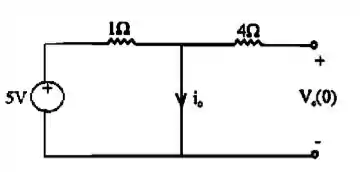
Daí é só separar em frações parciais e achar i_0 ( t )

I_o = (5)/(s) + (A)/(s) + (B s + C)/(s^2 + 1.2 s + 0.4) = (5)/(s) + (4 ( s + 1 ))/(s ( s^2 + 1.2 s + 0.4 ))

Vamos resolver essa parte da equação aqui (A)/(s) + (B s + C)/(s^2 + 1.2 s + 0.4)

(s^2 ( A + B ) + s ( 1.2 A + C ) + ( 0.4 A ))/(s ( s^2 + 1.2 s + 0.4 ))

Achando A , B e C :

A + B = 0 -> A = - B

1.2 A + C = 4

0.4 A = 4 -> A = 10

C = - 8

B = - 10

Agora substituímos os valores na equação:

I_o = (5)/(s) + (10)/(s) + (( - 10 s - 8 ))/(s^2 + 1.2 s + 0.4) = (15)/(s) - (10 ( s + 0.8 ))/(s^2 + 1.2 s + 0.4)

Completando os quadrados, teremos:

(15)/(s) - (10 ( s + 0.8 ))/(s^2 + 1.2 s + 0.4) = (15)/(s) - (10 s)/(( s + 0.6 )^2 + ( 0.2 )^2) - (8)/(( s + 0.6 )^2 + ( 0.2 )^2)

(15)/(s) - (10 ( s + 0.8 ))/(s^2 + 1.2 s + 0.4) = (15)/(s) - (10 s)/(( s + 0.6 )^2 + ( 0.2 )^2) - (0.2 xx 40)/(( s + 0.6 )^2 + ( 0.2 )^2)

Utilizando as fórmulas de Laplace, achamos a inversa chegando em i_o ( t )

e^(- a t) c o s omega t harr (s + a)/(( s + a )^2 + omega^2)

e^(- a t) s i n omega t harr (omega)/(( s + a )^2 + omega^2)

Chegamos em:

i_o ( t ) = 15 - 10 e^(- 0.6 t) c o s ( 0.2 t ) - 40 e^(- 6 t) s i n ( 0.2 t )

i_o ( t ) = 15 - 10 e^(- 0.6 t) ( c o s ( 0.2 t ) + 4 s i n ( 0.2 t ) ) , AA t > 0

Resposta

i_o ( t ) = 15 - 10 e^(- 0.6 t) ( c o s ( 0.2 t ) + 4 s i n ( 0.2 t ) ) , AA t > 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

105- Girador é um dispositivo para simular um indutor em um circuito. O circuito de um girador básico é apresentado na Figura 16.113 . Determinado a relação V i ( s ) / I o ( s ) , demonstre que a ind
103- Obtenha a função de transferência do circuito com A O P da Figura 16.112 na forma V o s V i s = a s s 2 + b s + c Onde a , b e c são constantes. Determine essas constantes.
104- Certo circuito possui uma admitância de entrada Y ( s ) . A admitância tem um polo em s = - 3 , um zero em s = - 1 e Y ∞ = 0.25S a ) Determine Y ( s ) b ) Uma bateria de 8V é conectada ao circuit
Aplique um fator de escala ao filtro passa-baixas ativo da figura, de modo que sua frequência de corte aumente de 1r a d / s para 200r a d / s . Use um capacitor de 1 m F .
Dado um circuito R L C em paralelo com R = 5 k Ω ,L = m HeC = 20 μ F , se o circuito sofrer a aplicação de fator de escala na amplitude de K m = 500 e na frequência de K f = 1 0 5 ,determine os valore