Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas Abrangentes - Ex. 105
105- Girador é um dispositivo para simular um indutor em um circuito. O circuito de um girador básico é apresentado na Figura Determinado a relação , demonstre que a indutância produzida pelo girador é .
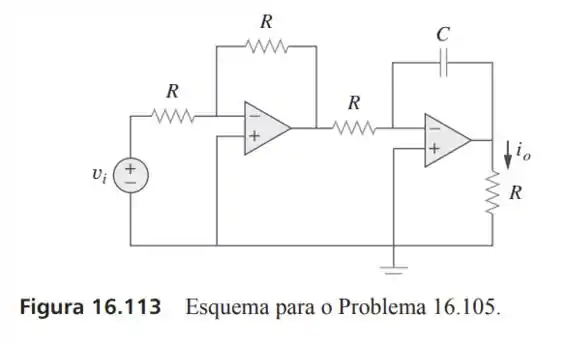
Passo 1
A tensão na saída do primeiro amplificador inversor será de:
Logo:
E a saída do segunda amplificador será:
Porém nossa variável de saída não é a tensão na saída no segundo amplificador e sim a corrente e essa corrente será:
Logo:
Passo 2
A impedância em um indutor pode ser escrita como a seguinte função de transferência:
E a impedância do circuito que encontramos será :
Logo a indutância desse circuito será por comparação:
Resposta
Exercícios de Livros Relacionados
Esboce as seguintes funções ax t = 10 ⋅ e - t ⋅ u t - 1 by t = 10 ⋅ e - t - 1 ⋅ u t cz t = cos 4 t ⋅ δ t - 1
A tensão em um indutor de 10m H é 15 ⋅ δ t - 2m V . Determine a corrente no indutor supondo que ele esteja inicialmente descarregado.
Um circuito é descrito por d i d t + 3 i = 2 ⋅ u t Determine i t para t0 , dado que i 0 = 0 .
Um circuito é descrito por 4 ⋅ d v d t + v = 10 a Qual a constante de tempo do circuito? b Qual é o v ∞ , valor final de v ? c Se v 0 = 2 , determine v t para t ≥ 0 .
Calcule as seguintes derivadas: a d d t [ u t - 1 ⋅ u t + 1 ] b d d t r t - 6 ⋅ u t - 2 c d d t s e n4 t ⋅ u t - 3