Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 69
Determine a admitância equivalente do circuito da figura 9.76.
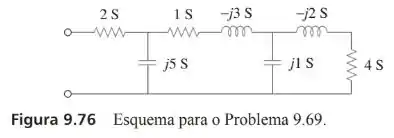
Passo 1
Como já temos no circuito que todos os componentes estão no domínio da frequência, temos que para encontrar ficou bem mais simples, basta fazermos uma associação de admitâncias em paralelo que é dada como nada mais nada menos como a soma das admitâncias individuais. Assim, comecemos encontrando a admitância equivalente para a parte mais a direita do nosso circuito, dessa forma, obteremos
Somando à essa admitância a do nosso capacitor vamos encontra
Prosseguindo, vamos pegar o circuito até antes do capacitor e vamos achar
Somando agora com a admitância do capacitor que havíamos pulados vamos encontrar
Agora, por fim, conseguimos encontrar o valor da nossa admitância equivalente final fazendo