Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 42
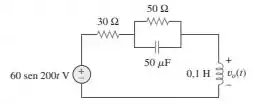
42. Calcule no circuito da figura
Passo 1
A primeira coisa que temos que fazer aqui é levar todos os elementos do circuito para a sua representação no circuito de impedâncias!
No final do próximo passo teremos esse circuito preenchido! Então venha comigo
Passo 2
No circuito nós temos:
- Uma fonte;
- dois resistores;
- um capacitor, e;
- um indutor.
- A fonte se transforma em um fasor de módulo e ângulo de fase , já que não tem ninguém somando com os ... Caso você esteja se perguntando “mas seno não é -90°?” Relaxa haha, explico melhor sobre no final dessa resolução!
- Os dois resistores se transformam nas impedâncias resistivas:
- O capacitor se transforma na impedância capacitiva através da fórmula (lembre-se de que micro é ):
- E o indutor se transforma em uma impedância indutiva:
Para transformar esses elementos para o circuito de impedância, observe que a frequência angular está definida pela fonte onde temos . Então teremos na transformação...
Podemos concluir então que o circuito de impedância será...
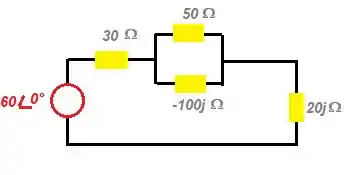
Passo 3
Repare que a impedância de está em paralelo com a impedância de , portanto...
Então...
Simplificando por ...
Multiplicando em cima e em baixo por ...
Se lembrando de que ...
Passo 4
Repare então que a gente pode encontrar a corrente facilmente agora fazendo a divisão da tensão pelo somatório das impedâncias...
A tensão em cima da impedância de então pode ser dada pela Lei de Ohm:
O número complexo pode ser visto como um ângulo de na forma polar:
Então a tensão pode ser então escrita como...
Para quem ficou em dúvida sobre ter usado para seno:
Então, tudo depende do referencial, na verdade. Vou te explicar: normalmente trabalhamos com os ângulos do cosseno e achamos a resposta em cosseno direto. Mas também podemos fazer isso com o seno. Por isso, você pode ver que o resultado está em seno, não em cosseno.
Você pode fazer as contas colocando -90° na fonte e verá que chega no mesmo resultado, mas ele aparece dessa forma:
Mas como , eles são o mesmo resultado. Beleza?