Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 67

Para ω = 10 3   r a d / s , determine a admitância de entrada em cada um dos circuitos da figura 9.74.

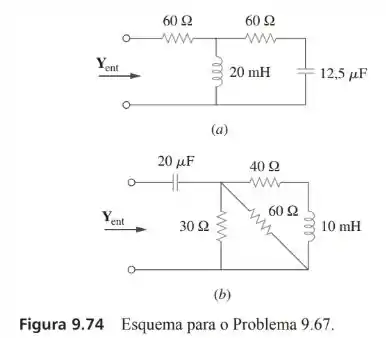
Passo 1

Vamos resolver primeiramente o circuito a e para isso, vamos transformar nossa indutância e capacitância para o domínio da frequência a partir da seguinte fórmula

20   m H → j ω L = j ⋅ 10 3 ⋅ 20 ⋅ 10 - 3 = j 20

12,5   μ F → 1 j ω C = 1 j ⋅ 10 3 ⋅ 12.5 ⋅ 10 - 6 = 1 j ⋅ 12.5 ⋅ 10 - 3 = - j 80

Dessa forma nossa impedância de entrada será

Z i n = 60 + j 20 | | 60 - j 80

Z i n = 60 + j 20 ⋅ 60 - j 80 j 20 + 60 - j 80 = 60 + j 1200 - 4800 60 - j 60

Lembrando-se que j é a unidade complexa/imaginária onde j 2 = - 1 . Então,

Z i n ≈ 63.33 + j 23.33 = 67.494 ∠ 20.22 °

Portanto, nossa admitância será dada por

Y i n = 1 Z i n = 1 67.494 ∠ 20.22 ° ≈ 14.8 ∠ - 20.22 °     m S

Passo 2

Para o circuito b procederemos da mesma maneira, então, temos

10   m H → j ω L = j ⋅ 10 3 ⋅ 10 ⋅ 10 - 3 = j 10

20   μ F → 1 j ω C = 1 j ⋅ 10 3 ⋅ 20 ⋅ 10 - 6 = 1 j ⋅ 20 ⋅ 10 - 3 = - j 5 0

Assim, podemos encontrar nossa impedância fazendo

Z i n = - j 50 + 20 | | 40 + j 10

Z i n = - j 50 + 20 ⋅ 40 + j 10 60 + j 10 = - j 50 + 20 ⋅ 41.231 ∠ 14.036 ° 60.828 ∠ 9.462 °  

Z i n = 13.51342 - j 48.9189 ≈ 50.751 ∠ - 74.56 °

Portanto, nossa admitância será dada por

Y i n = 1 Z i n = 1 50.751 ∠ - 74.56 ° = 5.246 + j 18.993   m S = 19.704 ∠ 74.56 °   m S

Resposta

a   Y i n = 1 Z i n = 14.8 ∠ - 20.22 °   m S

b   Y i n = 19.704 ∠ 74.56 °     m S

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a corrente i no circuito da Figura 9.42 quando v S t = 50 cos ⁡ 200 tV .
Determine v ( t ) no circuito R L C da Figura 9.48 .
Usando a figura 9.45 , elabore um problema para ajudar outros estudantes a entender melhor a admitância.
Para o circuito exibido na Figura 9.46 , determine Z e q e use esta para determinar a corrente I . Considere ω = 10r a d / s .
Usando a figura 9.43 , elabore um problema para ajudar outros estudantes a entenderem melhor a impedância.