Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 50

50- Determine v_x no circuito da Figura 9.57 . Considere i_s (t) = 5 cos (100 t + 40 °) A

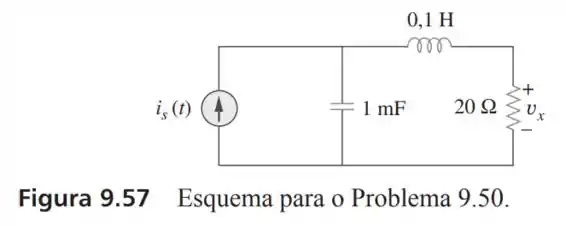
Passo 1

O circuito trabalha com uma frequência angular de omega = 100 r a d // s então a reatância no capacitor e no indutor serão de:

X_C = - (j)/(omega C) = - (j)/(10^(- 3) xx 100) = - j 10

X_L = j omega L = j (100 xx 0.1) = j 10

E o fasor dessa fonte de corrente será de:

i_s = 5 /_ 40 ° A

Isso nos deixa com o seguinte circuito:

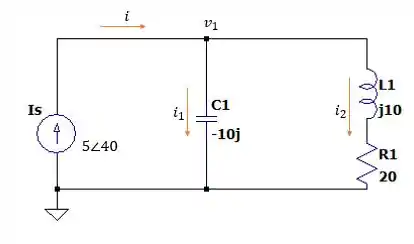
Onde para termos v_x precisamos encontrar i_2 .

Passo 2

E o valor de I_2 será calculado por:

(i_2)/(i_s) = (- 10 j)/(20 + j 10 - j 10)

i_2 = - (1)/(2) j xx 5 /_ 40 = 0.5 /_ - 90 xx 5 /_ 40 = 2.5 /_ - 50 ° A

Passo 3

Então a tensão no resistor de 20 omega será:

v_x = i_2 xx 20 = 50 /_ - 50 ° A

Em função de t temos:

v_x = 50 cos (100 t - 50 °) V

Pois é a mesma cara que a corrente

Resposta

v_x = 50 cos (100 t - 50 °) V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que os parâmetros de transmissão, A , B , C e D, definidos para o quadripolo da Fig. 14.12 como V 1 = A V 2 - B I 2 I 1 = C V 2 - D I 2 São dados por A = z 11 z 21 , B = Δ Z Z 21 C = 1 z 21 , D
O circuito mostrado é uma treliça com dois braços em série iguais a Z a e dois braços em cruz iguais a Z b . Este circuito é chamado treliça simétrica porque os braços em série são iguais e os braços
Demonstre que os circuitos dados são equivalentes ao quadripolo genérico. Note como os dois circuitos diferem
Mostre que o circuito dado é equivalente ao quadripolo genérico. Note como ele difere do circuito equivalente do Ex. 14.9.3
Calcule os parâmetros y da rede indicados. Coloque um resistor de 1 - Ω nos terminais de saída e calcule a funçăo de rede resultante V / - V 1