Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 35

Determine v_o ( t ) no circuito da figura.

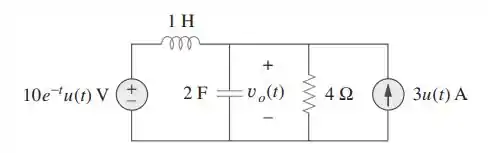
Passo 1

Redesenhando o circuito no domínio de Laplace, temos:

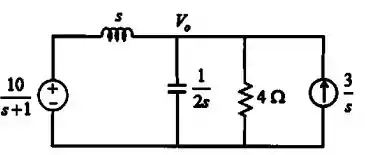
Passo 2

Utilizando a análise nodal no nó V_o encontraremos o V_o .

(V_o - (10)/(s + 1))/(s) + (V_o)/((1)/(2 s)) + (V_o)/(4) - (3)/(s) = 0

V_o = (3 s + 13)/(( s + 1 ) ( 2 s^2 + 0.25 s + 1 )_)

Passo 3

Separando em frações parciais teremos:

V_o = (3 s + 13)/(( s + 1 ) ( 2 s^2 + 0.25 s + 1 )_) = (A)/(s + 1) + (B s + c)/(2 s^2 + 0.25 s + 1)

Agora basta encontrar A , B e C :

A = 3.63636

B = - 7.27272

C = 9.36364

Daí, substituindo, teremos:

V_o = (3.63636)/(s + 1) + (- 7.27272 s + 9.36364)/(2 s^2 + 0.25 s + 1)

Simplificando…

V_o = (3.63636)/(s + 1) - 3.63636 (( s + 0.0625 )_)/(( s + 0.0625 )^2 + 0.70434) + 6.96977 (0.70434)/(( s + 0.0625 )^2 + 0.70434)

Por Laplace utilizando a tabela de transformadas, teremos:

v_o ( t ) = 3.63636 e^(- t) - 3.63636 e^(- 0.0625 t) c o s ( 0.70434 ) + 6.96977 e^(- 0.0625 t) s i n ( 0.7043 t ) u ( t ) V_

Resposta

v_o ( t ) = 3.63636 e^(- t) - 3.63636 e^(- 0.0625 t) c o s ( 0.70434 ) + 6.96977 e^(- 0.0625 t) s i n ( 0.7043 t ) u ( t ) V_

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(a) Se a chave na Figura 7.109 tiver sido aberta há um bom tempo e for fechada em t=0 , determine v o ( t ) . (b) Suponha que a chave se encontre fechada há um longo período e seja aberta emt=0 . Dete
Determine v 0 no circuito da Figura 7.112 quando v s=30 u ( t )V . Suponha que v 0 ( 0 )=5V .
Usando a Figura 7.108, elabore um problema para ajudar outros estudantes a entenderem melhor a resposta de um circuito RC.