Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 31

Obtenha v ( t ) e i ( t ) para t > 0 , no circuito da figura:

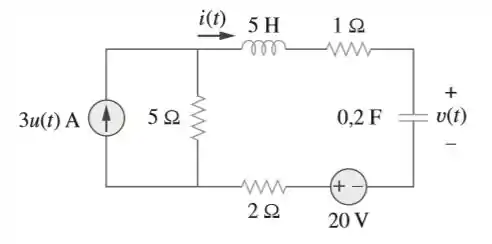
Passo 1

Para t < 0 o indutor funciona como um curto circuito e o capacitor funciona como um circuito aberto, então temos:

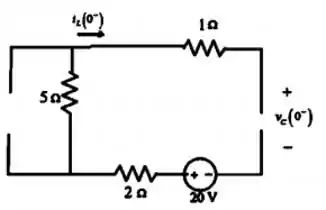
Passo 2

As condições iniciais serão:

i_L ( 0^- ) = 0 A_ no indutor

v_C_ ( 0^- ) = 20 V_ no capacitor

Passando tudo para Laplace, teremos este circuito:

Passo 3

Aplicando a Lei de Kirchhoff dos nós no nó de tensão V .

(3)/(s) = (V)/(5) + I_ ( s ) (1)

E aplicando a lei das tensões de Kirchhoff na malha 2 (Loop 2):

5 s I_ ( s ) + I_ ( s ) + (5)/(s) I_ ( s ) + (20)/(s) - (20)/(s) + 2 I_ ( s ) = V

Isolando para V , temos:

V = I ( s ) [(5 s^2 + 3 s + 5)/(s)]_ (2)

Passo 4

Agora, basta fazer os algebrismos substituindo a equação (2) na (1) e isolar I ( s ) e assim chegaremos em:

I ( s ) = (15)/(5 s^2^() + 8 s + 5)

Daí, vamos separar em frações parciais para utilizar o método das frações parciais e assim poder usar Laplace!!

I ( s ) = (15)/(5 s^2^() + 8 s + 5) = (A)/(( s - [- 0 . 8 + j 0.6_] )) + (B)/(( s - [- 0 . 8 - j 0.6_] ))

Agora basta encontrar A e B :

A = - j 12.5

B = j 12.5

Daí, substituindo, teremos:

I ( s ) = (- j 12.5)/(( s - [ - 0.8 + j 0.6 ] )) + (j 12.5)/(( s - [ - 0.8 - j 0.6 ] ))

Por Laplace utilizando a tabela de transformadas, teremos:

i ( t ) = [ - j 12.5 e^(( - 0.8 + j 0.6 ) t) + j 12.5 e^(( - 0.8 - j 0.6 ) t) ] u ( t ) A

Passo 5

Agora, vamos calcular a tensão que passa no capacitor:

V ( s ) = I ( s ) (1)/(s C) = (75)/(s [ s - ( - 0.8 + j 0.6 ) ] [ s - ( - 0.8 - j 0.6 ) ])

Passo 6

Daí, vamos separar em frações parciais para utilizar o método das frações parciais e assim poder usar Laplace!!

V ( s ) = (75)/(s [ s - ( - 0.8 + j 0.6 ) ] [ s - ( - 0.8 - j 0.6 ) ]) = (A)/([ s - ( - 0.8 + j 0.6 ) ]) + (B)/([ s - ( - 0.8 - j 0.6 ) ]) + (C)/(s)

Agora basta encontrar A , B e C :

A = - 37.5 + j 50

B = - 37.5 - j 50

C = 75

Daí, substituindo, teremos:

V ( s ) = (- 37.5 + j 50)/([ s - ( - 0.8 + j 0.6 ) ]) + (- 37.5 - j 50)/([ s - ( - 0.8 - j 0.6 ) ]) + (75)/(s)

Por Laplace utilizando a tabela de transformadas, teremos:

v ( t ) = [ ( - 37.5 + j 50 ) e^(( - 0.8 + j 0.6 ) t) + ( - 37.5 - j 50 ) e^(( - 0.8 - j 0.6 ) t) + 75 ] u ( t ) V

Resposta

i ( t ) = [ - j 12.5 e^(( - 0.8 + j 0.6 ) t) + j 12.5 e^(( - 0.8 - j 0.6 ) t) ] u ( t ) A

v ( t ) = [ ( - 37.5 + j 50 ) e^(( - 0.8 + j 0.6 ) t) + ( - 37.5 - j 50 ) e^(( - 0.8 - j 0.6 ) t) + 75 ] u ( t ) V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O circuito de cruzamento da figura é um filtro passa-baixas conectado a um woofer. Determine a função de transferência H ω = V 0 ω / V i ω .
Determinando circuito eletrônico para teste produziu uma curva ressonante com pontos de meia potência em 432 H z e 454 H z . Se Q = 20 , qual é a frequência de ressonância do circuito?
Um filtro passa-faixa de dupla sintonia e baixo fator de qualidade é mostrado na figura. Use PSpice ou MultiSim para gerar o gráfico de amplitude de V 0 ω .
O circuito R C na figura é usado para um compensador de avanço em um projeto de um sistema. Obtenha a função de transferência do circuito.
Em determinada aplicação, um filtro passa-baixas R C simples é projetado para reduzir o ruído de alta frequência. Se a frequência de corte desejada for 20k H z e C = 0,5μ F , determine o valor de R .