Usando a Figura 7.108, elabore um problema para ajudar outros estudantes a entenderem melhor a resposta de um circuito RC.
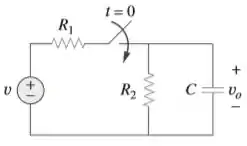
Passo 1
Haha, os papeis se inverteram hein? Vamo que vamo! Seria legal a gente modificar o circuito e encontrar a tensão para ! Primeiro, adicionando valores aos componentes:
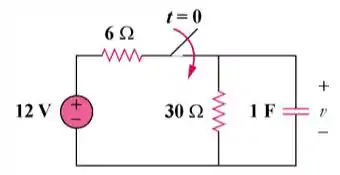
Passo 2
Agora é resolver a questão né? Bem, se queremos a tensão no capacitor para , primeiro vamos definir os valores de tensão para e !
Aplicando na formula para o circuito:
Passo 3
Aplicando a nossa famosa formula vinda da EDO:
Temos que,
E essa é a nossa questão!
Resposta
Ei, a resposta está no passo a passo :)