Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 56

Determine i_0 ( t ) para t > 0 no circuito da figura.

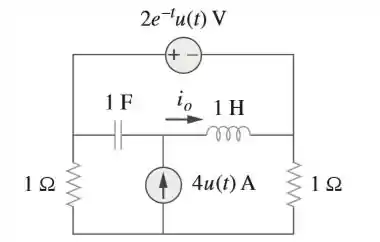
Passo 1

Vamos começar aplicando a análise de malhas ao circuito já desenhando no domínio de Laplace (s):

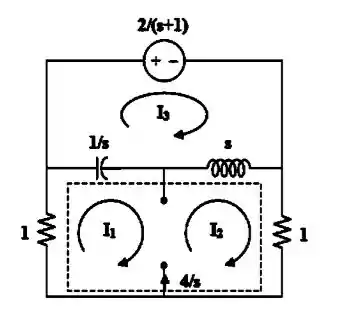
Passo 2

Na malha 3 teremos:

(2)/(s + 1) + (s + (1)/(s)) I_3 - (1)/(s) I_1 - s I_2 = 0

Na supermalha teremos:

(1 + (1)/(s)) I_1 + ( 1 + s ) I_2 - ((1)/(s) + s) I_3 = 0

Passo 3

Agora, vamos somar essas duas equações e teremos I_1 + I_2 = (- 2)/(( s + 1 ))

Mas, por análise nodal, sabemos que - I_1 + I_2 = (4)/(s)

Então, vamos juntar essas duas equações e isolar o I_2 e o I_1 , chegando em:

I_2 = ((2)/(s)) - (1)/(( s + 1 ))

I_1 = - ((2)/(s)) - ((1)/(s + 1))

Substituindo essas duas correntes la na expressão da malha 3, a gente vai isolar I_3 :

Então teremos:

I_3 = - (2)/(s) + (1.5 - 0.5 j)/(s + j) + (1.5 + 0.5 j)/(s - j)

Passo 4

Substituindo a equação I_1 + I_2 = (- 2)/(( s + 1 )) nas duas equações do Passo 2, teremos:

- (s + (1)/(s)) I_2 + (s + (1)/(s)) I_3 = (2 ( - s^2 + 2 s + 2 ))/(s^2 ( s + 1 ))

E daí é só resolver para I_o :

I_o = I_2 - I_3 = ((4)/(s)) - (1)/(s + 1) + ((- 1.5 + 0.5 j)/(s + j_)) + ((- 1.5 - 0.5 j)/(s - j_))

ou, resolvendo com Laplace inversa:

i_o ( t ) = [4 - e^(- t) + 1.5811 e^(- j t + 161.57 °) + 1.5811 e^(j t - 161.57 °)] u ( t ) A_

Resposta

i_o ( t ) = [4 - e^(- t) + 1.5811 e^(- j t + 161.57 °) + 1.5811 e^(j t - 161.57 °)] u ( t ) A_

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Obtenha o gráfico de amplitude da resposta V 0 do circuito da figura para o intervalo de frequências 100f1000H z .
Use o PSpice ou MultiSim para obter a resposta de frequência da figura.
Use o PSpice ou MultiSim para obter os gráficos de amplitude e de fase de V 0 I s do circuito da Figura.
No intervalo 0,1f100 H z , represente graficamente a resposta do circuito na figura. Classifique esse filtro e obtenha ω 0 .
Se i s t = e - 2 t u t A no circuito mostrado na figura. Determine o valor de i 0 t .