Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 58

Considere a Figura 16.81 e elabore um problema para ajudar outros estudantes a entender melhor a análise de circuitos no domínio s em circuitos com fontes dependentes.

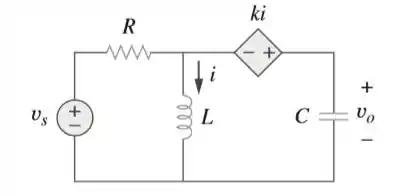
Passo 1

Vamos criar um problema com valores reais:

Na figura temos i ( 0 ) = 1 A ,   v o ( 0 ) = 2 V e v s = 4 e - 2 t u ( t ) V . Queremos encontrar v o ( t ) , para t > 0 .

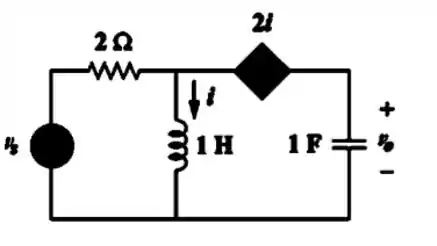
Passo 2

Primeiro vamos incorporar as condições iniciais ao circuito no domínio de Laplace (s):

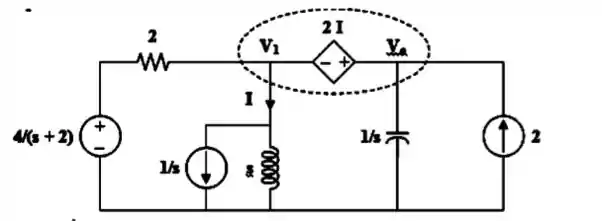
Passo 3

Em seguida, no supernó, vamos usar a lei dos nós e usando algebrismos, vamos chegar numa expressão para V o , observe:

4 s + 2 - V 1 2 + 2 = V 1 s + 1 s + s V o

2 s + 2 + 2 = 1 2 + 1 s V 1 + 1 s + s V o (1)

Mas como V o = V 1 + 2 I e I = V 1 + 1 s

Então,

V o = V 1 + 2 ( V 1 + 1 ) s → V 1 = V o - 2 s s + 2 s = s V o - 2 s + 2 (2)

Passo 4

Agora, vamos substituir a equação (2) na (1) para assim encontrarmos uma expressão para V o .

2 s + 2 + 2 - 1 s = s + 2 2 s s s + 2 V o - 2 s + 2 + s V o

2 s + 2 + 2 - 1 s + 1 s = 1 2 + s V o

2 s + 4 + 2 ( s + 2 ) = 2 s + 6 s + 2 = s + 1 2 V o

Agora, vamos separar em frações parciais para achar a expressão no domínio do tempo:

2 s + 6 s + 2 s + 1 2 = V o = A s + 1 2 + B s + 2

Achando A:

( - 1 + 6 ) ( - 0.5 + 2 ) = 3.333

Achando B:

- 4 + 6 ( - 2 + 1 2 ) =   - 1.3333

V o = 3.333 s + 1 2 - 1.3333 s + 2

Pronto, daí fica fácil usar nossa tabela de laplace e resolvê-la no domínio do tempo!

e - a t f ( t ) ↔ F ( s + a )

Fazendo pra nossa expressão:

v o ( t ) = ( 3.333 e - t 2 - 1.3333 e - 2 t ) u ( t ) V ,   ∀   t > 0

Resposta

v o ( t ) = ( 3.333 e - t 2 - 1.3333 e - 2 t ) u ( t ) V ,   ∀   t > 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um circuito RLC em paralelo tem R = 5 k Ω , L = 8 m H , e C = 60 µ F µ Determine:(a) A frequência de ressonância.(b) A largura de banda.(c) O fator de qualidade.
Espera-se que um circuito ressonante R L C em paralelo tenha uma admitância de faixa média igual a 25 ×10 - 3S , um fator de qualidade 80 e uma frequência de ressonância 200 k r a d s . Calcule os val
Um circuito R L C em paralelo é ressonante em 5,6M H z , tem um fator Q igual a 80 e um ramo resistivo de 40 k Ω . Determine os valores de LeC nos outros dois ramos.
Um circuito ressonante em paralelo tem resistência de 2k Ω e frequências de meia potência de 86k H z e 90k H z . Determine:(a) A capacitância.(b) A indutância.(c) A frequência de ressonância.(d) A lar
Considere o circuito “tanque” da F i g u r a14.79 e determine a frequência de ressonância