Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 57

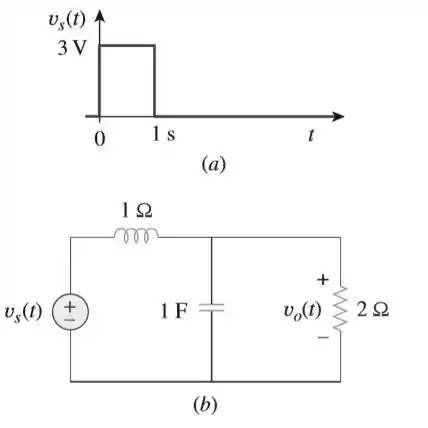
  1. Determine a transformada de Laplace da tensão mostrada na figura.
  2. Usando o valor de v s ( t ) no circuito mostrado na figura, determine o valor de v o ( t ) .

Passo 1

Temos,

V s ( t ) = u ( t ) - 3 u ( t - 1 )

ou

V s = 3 s - e - s s = 3 s ( 1 - e - s )

Desenhando o circuito no domínio de Laplace (s):

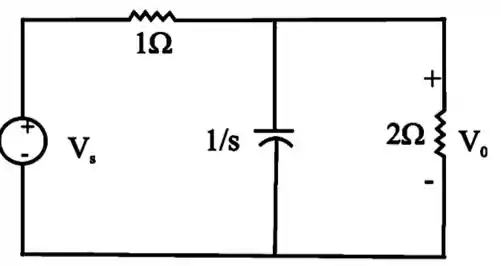
Passo 2

Fazendo análise nodal:

V o - V s 1 + s V o + V o 2 = 0 → ( s + 1.5 ) V o = V s

V o = 3 s ( s + 1.5 ) ( 1 - e - s )

V o = 2 s - 2 s + 1.5

E por fim, a gente faz o Laplace para passar essa tensão para domínio do tempo usando:

e - a t f ( t ) ↔ F ( s + a )

u ( t ) ↔ 1 s

t ↔ 1 s 2

Chegamos em:

v o ( t ) = 2 - 2 e - 1.5 t u ( t ) - ( 2 - 2 e - 1.5 ( t - 1 ) ) u ( t - 1 ) V

Resposta

v o ( t ) = 2 - 2 e - 1.5 t u ( t ) - ( 2 - 2 e - 1.5 ( t - 1 ) ) u ( t - 1 ) V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Projete um circuito ressonante R L C em série com ω 0 = 40r a d / s e B = 10r a d / s .
Elabore um problema para ajudar outros estudantes a entender melhor ω 0 , Q e B na ressonância em circuitos R L C em série.
Seja v s = 20 cos ⁡ a t V no circuito da Figura. Determine ω 0 , Q e B , visto pelo capacitor.
Um circuito R L C em série tem R = 2 k Ω , L = 40 m H e C = 1μ F . Calcule a impedância na ressonância para frequências de um quarto, metade, o dobro e quatro vezes a frequência de ressonância.
Projete um circuito R L C em série com B = 20r a d / s e ω 0 = 1000r a d / s . Determine o Q do circuito. Faça R = 10Ω .