Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 23

Se M = 0,2   H e v s = 12 cos ⁡ 10 t   V no circuito da Figura 13.92 , determine i 1 e i 2 . Calcule a energia armazenada nas bobinas acopladas em t = 15   m s .

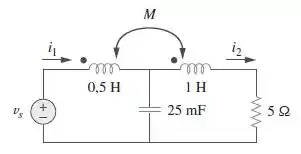
Passo 1

Bom, galerinha, a primeira coisa que vamos fazer é passar os elementos do circuito do domínio do tempo para o domínio da frequência:

L 1 = 0,5   H   →     X L 1 = j ω L 1 = j 5   Ω

L 2 = 1,0   H   →     X L 2 = j ω L 2 = j 10   Ω

M = 0,2   H   →     X M = j ω M = j 2   Ω

C = 25   m F   →     X C = 1 j ω C = - j 4   Ω

Observando o circuito abaixo, vamos aplicar a lei das malhas em cada uma delas.

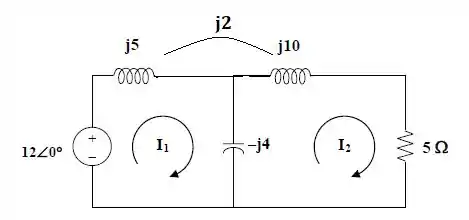
Aplicando a lei das malhas para a malha 1 ,

- 12 + j 5 I 1 + j 2 I 2 + - j 4 I 1 - I 2 = 0

j I 1 + j 6 I 2 = 12 … ( 1 )

Para a malha 2 ,

- j 4 I 2 - I 1 + j 10 I 2 + j 2 I 1 + 5 I 2 = 0

j 6 I 1 + 5 + j 6 I 2 = 0 … ( 2 )

Passo 2

Da equação ( 1 ) :

I 1 = - j 12 - 6 I 2 … ( 3 )

Substituindo a equação ( 3 ) na equação ( 2 ) :

j 6 - j 12 - 6 I 2 + 5 + j 6 I 2 = 0

72 + 5 + j 6 - j 36 I 2 = 0

72 + 5 - j 30 I 2 = 0

I 2 = - 0.39 - j 2,33

I 2 = 2,36 ∠ - 99,46 °   A

Substituindo esse valor na equação ( 1 ) :

j I 1 + j 6 ( - 0,39 - j 2,33 ) = 12

I 1 = - j 12 - 6 - 0,39 - j 2,33

I 1 = 2,33 + j - 12 + 14,01

I 1 = 2,33 + j 2,01 = 3,081 ∠ 40,74 °   A

Passo 3

Passando para o domínio do tempo,

i 1 t = 3,081 cos ⁡ 10 t + 40,74 °   A

i 2 t = 2,36 cos ⁡ 10 t - 99,46 °   A

No instante t = 15   m s ,

10 t = 10 × 15 × 10 - 3 = 0,15   r a d = 8,59 °

i 1 = 3,081 cos ⁡ 49,33 ° = 2,007   A

i 2 = 2,36 cos ⁡ ( - 90,87 ° ) = - 0,036   A

A energia armazenada nas bobinas acopladas é igual a:

w = 1 2 5 2,007 2 + 1 2 1 - 0,036 2 - 0,2 2,007 - 0,036

w = 10,07 + 0,000648 + 0,01444

w = 10,094   J

Resposta

As correntes são iguais a:

i 1 t = 3,081 cos ⁡ 10 t + 40,74 °   A

i 2 t = 2,36 cos ⁡ 10 t - 99,46 °   A

A energia armazenada é igual a:

w = 10,094   J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine as correntes I 1 , I 2 e I 3 no circuito da Figura abaixo. Determine a energia armazenada nas bobinas acopladas em t = 2m s . Adote ω = 1.000r a d / s .
Considere a Figura abaixo e elabore um problema para ajudar outros estudantes a entender melhor a energia em circuitos acoplados.
Detemrine I 0 no circuito da Figura 13.95 . Inverta o ponto no enrolamento da direita e calcule I 0 novamente.
Como mostra a perspectiva prática, o projeto de autocapacitância não permite uma verdadeira tela de múltiplos toques – se a tela é tocada em dois pontos, quatro locais de contato são identificados: do