Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 35
Determine a corrente no circuito da Figura quando .
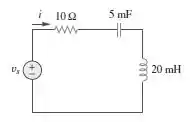
Passo 1
Galerinha, como temos um circuito série, a corrente que percorre o circuito pode ser facilmente encontrada dividindo a tensão da fonte de entrada pela impedância total do circuito! Primeiro, vamos passar os componentes para o domínio da frequência:
Assim, a impedância total do circuito é igual a:
Passo 2
Uma vez que temos todos os componentes no domínio da frequência, podemos fazer nossa conta!
Voltando para o domínio do tempo:
Resposta
A corrente é igual a:
Exercícios de Livros Relacionados
Uma bobina de impedância 8 + j 6Ω é ligada em série com uma reatância capacitiva X . A associação em série é conectada em paralelo com um resistor R . Dado que a impedância equivalente do circuito res
Consulte o circuito R C da figura 9.81. a Calcule o deslocamento de fase em 2M H z . b Determine a frequência em que o deslocamento de fase é 45 ° .
Considere o circuito comutador de fase da figura 9.83. Seja V i = 120 V , operando a 60 H z . Determine: a V 0 quando R é máxima. b V 0 quando R é mínima. c O valor de R que produzirá um deslocamento
a Calcule o deslocamento de fase do circuito da Figura 9.82. b Informe se o deslocamento de fase está avançado ou atrasado (saída em relação à entrada). c Determine a magnitude da saída quando a entra
Uma ponte de capacitância está equilibrada quando R 1 = 1 00Ω ,R 2 = 2 k ΩeC s = 40μ F . Qual o valor de C x , a capacitância do capacitor em teste?