Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 34
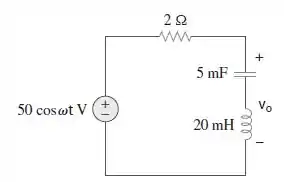
Qual é o valor de que fará que a resposta forçada, , na figura , seja zero?
Passo 1
Galerinha, a tensão é a soma das tensões do capacitor e do indutor, certo? A única maneira disso ser igual a zero é se elas forem iguais e com sinais opostos, ou seja:
A tensão no capacitor pode ser escrita como:
A tensão no indutor pode ser escrita como:
Substituindo esses valores na equação , temos:
Passo 2
Vamos isolar o na equação:
Substituindo os valores, temos:
Resposta
O valor da frequência angular deve ser:
Exercícios de Livros Relacionados
No Ex. 10.2.2, substitua a fonte de corrente por i 1 = I m e j ω t A e demonstre que a resposta v 1 tem a propriedade que Re v 1 = v , onde v é a resposta original.
Demonstre que, para a real, R e a d x d t = a d d t ( R e x ) e use este resultado para verificar (10.22). (Sugestāo: faça x = f + j g , onde f e g são reais.)
Troque a função de excitaçảo real I m c o s ω t no Ex. 10.2 . 2 pela funçáo de excitaçăo complexa I m e jwl . Calcule a resposta complexa resultante v 1 e mostre que a resposta real é v = R e v 1
(a) Das equações no domínio do tempo, calcule a resposta forçada v se v g = 10 e β tV .
Determinar se v 1 está adiantada ou atrasada em relaçáo a v 2 e de quanto.(a) v 1 = 3 c o s 4 t - 30 ∘ , v 2 = 5 s e n 4 t ,