Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 36

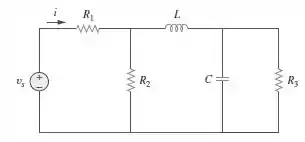
Usando a figura 9.43 , elabore um problema para ajudar outros estudantes a entenderem melhor a impedância.

Passo 1

Pessoal, vamos resolver a seguinte questão:

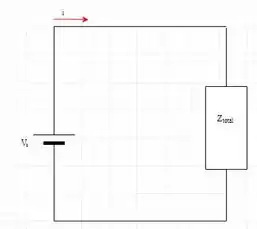
“Dado o circuito, calcule a corrente i .”

Bom, o interessante aqui seria encontrarmos a impedância equivalente desse ciruito primeiro, pois uma vez que tivermos Z e q , para encontrar a corrente i seria apenas necessário dividir o valor de v S por Z e q . Então, mãos à obra!

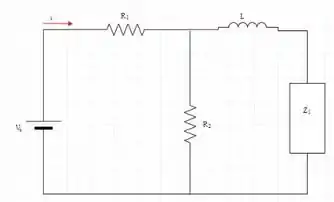
Vamos chamar de Z 1 a impedância resultante do cálculo de R 3 // C . Assim,

Z 1 = R 3 × 1 j ω C R 3 + 1 j ω C = R 3 1 + j ω R 3 C

Passo 2

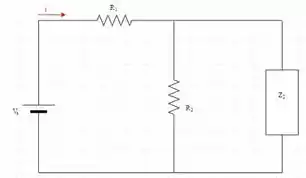
Vamos chamar de Z 2 a impedância resultante da associação série de L e Z 1 . Assim,

Z 2 = L + Z 1

Z 2 = L + R 3 1 + j ω R 3 C

Passo 3

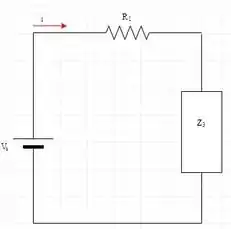
Vamos chamar de Z 3 impedância resultante do cálculo de R 2 // Z 2 . Assim,

Z 3 = R 2 × L + R 3 1 + j ω R 3 C R 2 + L + R 3 1 + j ω R 3 C

Passo 4

Por fim, a impedância total Z t o t a l pode ser aclacualda a través da associação série entre Z 3 e R 1 :

Z t o t a l = R 1 + R 2 × L + R 3 1 + j ω R 3 C R 2 + L + R 3 1 + j ω R 3 C

Portanto, a corrente que circula pelo circuito pode ser calculada através da seguinte equação:

i = V s Z t o t a l

i = V S R 1 + R 2 × L + R 3 1 + j ω R 3 C R 2 + L + R 3 1 + j ω R 3 C

i = V S R 2 + L + R 3 1 + j ω R 3 C R 1 R 2 + L + R 3 1 + j ω R 3 C + R 2 L + R 3 1 + j ω R 3 C

Resposta

A corrente é igual a:

i = V S R 2 + L + R 3 1 + j ω R 3 C R 1 R 2 + L + R 3 1 + j ω R 3 C + R 2 L + R 3 1 + j ω R 3 C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que se Z 1 = Z 3 , Z 4 = Z 2 , Z 5 no circuito “ponte” mostrado, então I = V = 0 e, portanto, todas as outras correntes e tensões permanecem inalteradas para qualquer valor de Z 5 . Logo, ela p
Calcule o valor de v em regime permanente.
Calcule a corrente i em regime permanente, se i_g = 9 - 20 cos t - 39 cos 2 t + 18 cos 3 t A .
Demonstre quY = Y_1 + (1)/(Z_2 + (1)/(Y_3 + (1)/(Z_4 + (1)/(Y_5)))) (Sugestão: Observe que Y = Y_1 + Y_a = Y_1 + 1 // Z_a = Y_1 + 1 // ( Z_2 + Z_b ) = ... )
Calcule v ( t ) , se (a) V ( s ) = 6 /_ 10^@ com s = - 2 + j 8 ; (b) V ( s ) = 5 /_ 0^@ c o m s = - 10 ; (c) V ( s ) = 4 + j 3 com s = - 1 + j 2 e (d) V ( s ) = - j 6 com s = j 4 .