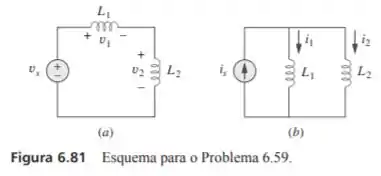
Para dois indutores em série como aqueles mostrados na figura 6.81ª, demonstre que o princípio da divisão da tensão é
Supondo que as condições iniciais sejam zero.
Para dois indutores em paralelo como aqueles apresentados na figura 6.81b, demonstre que o princípio da divisão da corrente é
Supondo que as condições iniciais sejam zero.
Passo 1
Para o primeiro caso vamos ter
Da equação do indutor para cada um dos indutores vamos ter
Portanto, temos
Como queríamos demonstrar
Passo 2
Já para o segundo caso vamos ter
Sendo assim, temos
De temos que
Fazendo o mesmo para vamos obter
Resposta
Ei, a resposta está no passo a passo :)