Calculei para t0 , se o circuito está em regime permanente em t = 0 - .

i t = 2,5 e - 8 t + e - 4 t A .

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.Problemas - Ex. 20

Calcule para , se o circuito está em regime permanente em .

Passo 1

Iae, meus queridos!! Td blzinha?

Essa questão é bem tranquila, nada que já não tenhamos visto.

Quando , o circuito se comporta da seguinte forma.

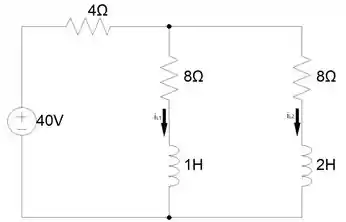
A princípio, temos que calcular os valores iniciais das correntes de cada indutor. A questão nos disse que em , o circuito está em regime permanente, portanto, podemos considerar os indutores como fios ideais.

Para calcular os valores das correntes iniciais, temos que calcular a corrente gerada pela fonte e após isso, usar o método de divisão de corrente.

As resistências associadas a e , são de mesmo valor, portanto:

Passo 2

Quando , o circuito terá a seguinte configuração:

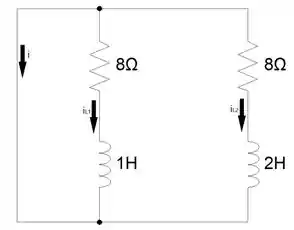
Analisando o circuito, podemos afirmar que . Sendo assim, podemos imaginar o circuito como sendo duas malhas distintas e somar os valores das correntes e .

Por fim:

Achou fácil? Bora pra outra!

Resposta

Exercícios de Livros Relacionados

A chave do circuito mostrado na Figura P7.36 esteve na posição a por um longo tempo antes de passar para a posição b em t = 0. a) Determine as expressões numéricas para i L(t) e vo (t) quando t $ 0. b

A chave do circuito mostrado na Figura P7.37 esteve na posição a por um longo tempo. Em t = 0, ela passa instantaneamente para a posição b. a) Determine a expressão numérica para i o (t) quando t $ 0.

A corrente e a tensão nos terminais do indutor no circuito da Figura 7.16 são i(t) = (4 + 4e-40t ) A, t $ 0; v(t) = -80e-40t V, t $ 0+. a) Especifique os valores numéricos de Vs , R, Io e L. b) Em qua

a) Use os valores dos componentes do Apêndice H para criar um circuito RL de primeira ordem (veja a Figura 7.16) com uma constante de tempo de 8 ms. Use um único indutor e uma rede de resistores, se n

Repita o Problema 7.37, assumindo que a chave no circuito da Figura P7.37 esteve na posição b por um longo tempo e passa para a posição a em t = 0, onde permanece.