Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.7 - Ex. 3
Usando funções degrau unitário, escreva uma expressão para para .
Passo 1
Fala galera! Tudo bem com vocês? Vamos resolver esta questão de elétrica.
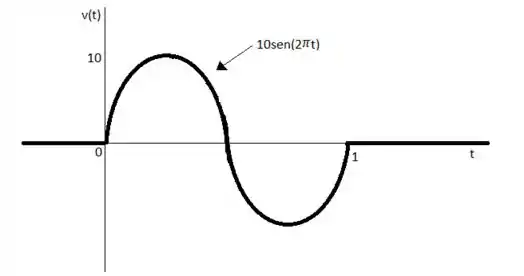
De acordo com os dados fornecidos pelo enunciado da questão e pela figura, sabemos que o domínio de t faz parte de todo os números reais, então devemos desenvolver uma expressão onde se pode considerar esse domínio de função.
Também sabemos que em certo intervalo de valores de t o valor da função é de , então também devemos considerar esse valor quando formos escrever a função. Então bora lá.
Considerando que o intervalo mencionado anteriormente é de , podemos escrever a função da seguinte forma:
Passo 2
Agora que temos a função escrita dessa forma, podemos trabalhar com ela para escrever a função degrau unitário que corresponde a essa expressão. Pelos dados anteriores temos o seguinte:
Substituindo os valores encontrados teremos a seguinte resposta: