Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 4.Problemas - Ex. 82

O resistor variável no circuito da Figura P4.82 é ajustado para a máxima transferência de potência a R 0 .

a) Determine o valor de R 0 .

b) Determine a potência máxima que pode ser transferida para R 0 .

c) Encontre um resistor no Apêndice H com valor mais próximo do obtido em (a). Qual a potência transferida para esse resistor?

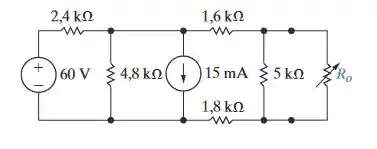
Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

A - A máxima transferência de potência ocorre quando a resistência da carga é igual à resistência de Thévenin ( R t h ) .

Portanto, para obter o R 0 necessário para a transferência máxima de potência, temos que obter R t h . Para calcular R t h , vamos desativar todas as fontes independentes por curto-circuito em todas as fontes de tensão e circuito aberto em todas as fontes de corrente. Em seguida, calcular a resistência vista olhando para a rede no par de terminais designado.

R t h = 5   k Ω       1,6 k Ω + 2,4 k Ω       4,8 k Ω ) + 1,8 k Ω )

Com isso, nós temos que

R t h = 5000 ( 1600 + 2400 ∙ 4800 2400 + 4800 + 1800 ) 5000 + 1600 + 2400 ∙ 4800 2400 + 4800 + 1800

Fazendo os cálculos, nós temos que

R t h = 2500   Ω

Portanto,

R 0 = R t h = 2500   Ω

Passo 2

B - Para obter a potência máxima entregue a R 0 , temos que calcular V t h . Vamos obter V t h aplicando o método das correntes de malha, temos uma supermalha, então temos que saber a relação de correntes através da fonte de corrente, com isso, nós temos que

i 2 - i 3 = 0,015   ( 1 )

E aplicando o método para a super malha, nós temos que

4800 i 2 - i 1 + 1600 i 3 + 5000 i 3 + 1800 i 3 = 0

Simplificando

- 4800 i 1 + 4800 i 2 + 8400 i 3 = 0   ( 2 )

Aplicando o método das correntes de malha na malha mais à esquerda, nós obtemos o seguinte resultado

- 60 + 2400 i 1 + 4800 i 1 - i 2 = 0

Simplificando novamente, nós temos que

7200 i 1 - 4800 i 2 = 60   ( 3 )

Resolvendo este sistema, nós temos que

i 1 = 19,4   m A

i 2 = 16,6   m A

i 3 = 1,6   m A

Calculando V t h

V t h = 5000 i 3 = 8   V

E consequentemente, calculando a potência máxima entregue a R 0

P m á x = V t h 2 4 R t h

Substituindo os valores, nós temos que

P m á x = 8 2 4 ( 2500 ) = 6,4   m W

Passo 3

C – O valor do resistor mais próximo do valor de R t h encontrado na letra (a) é 2,7   k Ω , vamos calcular a potência entregue a 2,7   k Ω

P = V t h R 0 + R t h 2 R 0

Substituindo os valores, nós temos que

P = 8 2700 + 2500 2 2700 = 6,391   m W

Logo

P = 6,391   m W

Resposta

a )   R 0 = 2500   Ω

b )   P m á x = 6,4   m W

c )   P = 6,391   m W

Exercícios de Livros Relacionados

69- Determine a potência máxima transferida para o resistor R no circuito da Figura 4.135
95- Um voltímetro C C com sensibilidade de 20k Ω / V é usado para encontrar o equivalente de Thévenin de um circuito linear. As leituras em duas escalas são as seguintes: ( a ) Escala 0 - 10V : 4V ( b
94- Atenuador é um circuito de interface que reduz o nível de tensão sem mudar a resistência de saída. ( a ) Através da especificação de R s e R p na interface da Figura 4.150 , projete um atenuador q
96- Um conjunto de resistências é conectado a um resistor de carga R e uma bateria de 9V conforme mostrado na Figura 4.151 . ( a ) Determine o valor de R tal que V o = 1.8V ( b ) Calcule o valor de R
98- Para o Problema prático 4.18 , determine a corrente através do resistor de 40Ω e a potência dissipada pelo resistor.