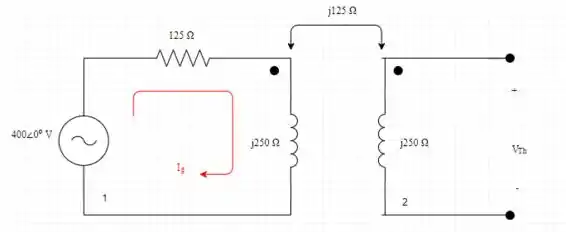
- Determine a expressão de regime permanente para as correntes i g e i L no circuito da Figura P10.55, quando vg = 400 cos 400t V.
- Determine o coeficiente de acoplamento.
- c) Determine a energia armazenada nos enrolamentos magneticamente acoplados em t = 1,25p ms e t = 2,5p ms.
- d) Determine a potência fornecida ao resistor de 375 V.
- e) Se o resistor de 375 V for substituído por um resistor variável RL, qual será o valor de RL para que ele absorva a máxima potência média?
- f) Qual é a máxima potência média em (e)?
- g) Admita que o resistor de 375 V seja substituído por uma impedância variável ZL. Qual é o valor de ZL para que ela absorva a máxima potência média?
- h) Qual é a máxima potência média em (g)?
Passo 1
Beleza pessoal?! Vamos começar nossa maratona, pegue sua garrafa de água e seu tênis e vem comigo.
- Primeiro iremos determinar a impedância de dois indutores de 625 mH
- O coeficiente de acoplamento k é dado por
- Em
- A potência transferida é dada por
- Desconecte a carga conforme mostrado na Figura 1 e determine a tensão equivalente de Thevenin V_{T} nos terminais de carga
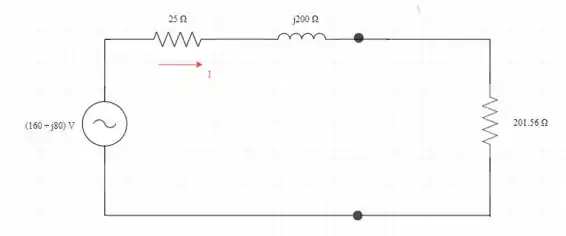
- Conecte o resistor de carga 201,56 ao circuito equivalente de Thevenin, conforme mostrado na Figura 3
- A potência média máxima é transferida para a impedância de carga quando a impedância de carga é combinada com a impedância equivalente de Thevenin
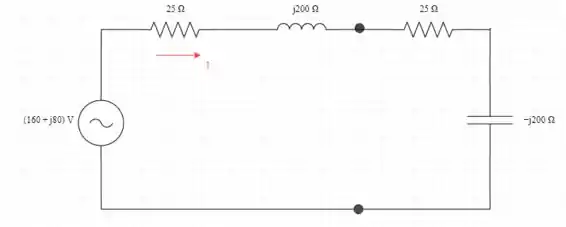
- Conecte a impedância de carga 25 - j200 ao circuito equivalente de Thevenin, conforme mostrado na figura
Determinar agora a impedância do indutor de
Agora iremos escrever as equações das duas malhas
Onde = é a corrente da malha da fonte de tensão
é a corrente da malha de carga
Substituindo (2) em (1) para determinar
Determinando em (2)
Determine a expressão de regime permanente para as duas correntes e
Passo 2
O ângulo 400t é dado por
A corrente da fonte é dada por
A corrente da carga é dada por
A energia armazenada nas bobinas acopladas magneticamente é dada
Em
O ângulo 400t é dado por
A corrente da fonte é dada por
A corrente da carga é dada por
A energia armazenada nas bobinas acopladas magneticamente é dada
Passo 3
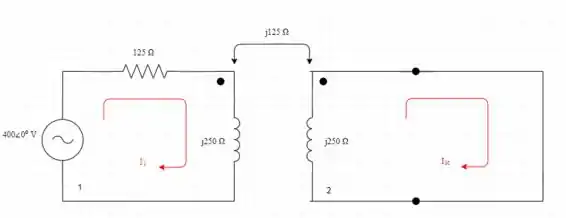
Conecte os terminais de carga por meio de um curto-circuito, conforme mostrado na Figura 2
Escrevendo agora a equação das duas malhas
Substituindo (5) em (4)
determine a impedância equivalente de Thévenin
Se apenas a magnitude da impedância da carga estiver variando, a maior parte da potência média é transferida para a carga.
Portanto, o valor de que produzirá a máxima transferência de potência média é dado por
Passo 4
Determine a corrente que flui através da carga I
A potência é dada por
Determine o valor da impedância de carga que produzirá a transferência de potência média máxima
Determine a corrente que flui através da carga I
Agora iremos finalmente calcular a potência
Resposta
- K = 0.5