Determine a frequência central e a largura de banda dos filtros passa-faixa na Figura 14.88
Letra a)
Passo 1
Letra a) Filtro passa-faixa composto por um circuito com Resistores e capacitores
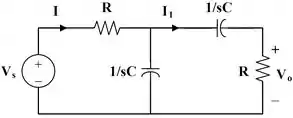
Se liga ai! O circuito é o observado abaixo. Primeiramente vamos nomear duas correntes neste circuito, são estas a corrente total e a corrente que irá circular pela saída. Outro passo importante é passar todos os componentes para suas respectivas impedâncias
Passo 2
Vamos determinar a impedância total do circuito definida como Primeiro vamos encontrar composto pela associação em série do capacitor com resistor final
Em seguida esta associação estará em paralelo com o primeiro capacitor, logo
Que resultará em
Somado ao primeiro resistor em série com
Logo
Passo 3
Com podemos encontrar pela lei de Ohm
E a corrente que passa pelo capacitor e resistor final pode ser encontrada pelo divisor de corrente
Como a tensão é encontrada por
Logo também é
Passo 4
Igualando o encontrado no passo 3
Obteremos
Passo 5
Substituindo
Simplificando e organizando termo a termo
Passo 6
O passo seguinte é colocar a função de transferência na forma padrão do filtro passa-faixa
Dividindo a expressão encontrada no passo anterior por
Multiplicando em cima e em baixo por e em seguida colocando em evidência, obteremos finalmente
Desta forma, por comparação a largura de banda será
Como e
E a frequência central
Resposta
Letra a)
A largura de banda é
A frequência central é igual a