Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas - Ex. 29
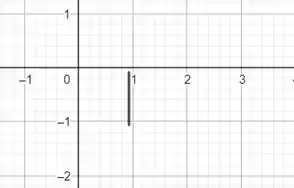
Esboce as seguintes funções
Passo 1
Para os dois primeiros gráficos temos que a função degrau está ali para mostrar que o gráfico irá começar em para a letra e em para a letra , haja vista que o degrau é para todo tempo antes do valor que zera seu argumento. Assim, atentando-nos para esses detalhes basta que plotemos os gráficos das exponenciais multiplicadas pelos escalares obtendo, assim,
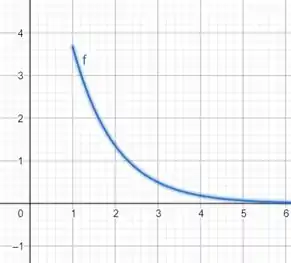
Passo 2
Por fim, para o último item como temos um impulso cujo argumento é , ou seja, vamos ter um pico em que vai ser multiplicado por que é o valor de em radianos. Então, nosso gráfico fica sendo
Resposta
Exercícios de Livros Relacionados
Determine a transformada de Laplace da tensão mostrada na figura. Usando o valor de v s ( t ) no circuito mostrado na figura, determine o valor de v o ( t ) .
Considere o circuito RLC mostrado na figura e determine a resposta completa se v ( 0 ) = 2V quando a chave é fechada.
Determine i 0 ( t ) para t0 no circuito da figura.
A função na figura é movida da posição 1 para a 2 em t = 0 . Determine v ( t ) para todo t0 .
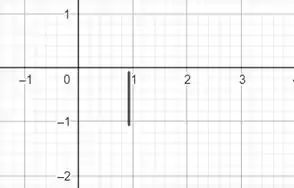
Considere o circuito RLC em paralelo da figura. Determine v ( t )ei ( t ) dado que v ( 0 ) = 5 e i ( 0 ) = 2A