Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 11.Problemas - Ex. 50

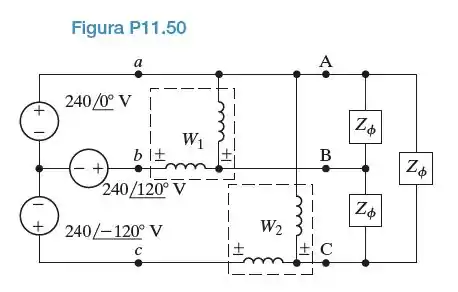
a) Determine a leitura de cada wattímetro no circuito da Figura P11.50. O valor de Z ϕ é

40/-30° / Ω .

b) Verifique se a soma das leituras dos wattímetros é igual à potência média total fornecida à carga ligada em ∆ .

Passo 1

Falaaa, pessoal! Como vocês estão?

Bora pra mais uma questãozinha pra exercitar o que a gente sabe circuitos trifásicos equilibrados!

  1. Temos que:

    2. W 1 = V B A I b B c o s θ

    W 2 = V C A I c C c o s θ

    Para uma sequência de fase negativa, temos que:

    V B A = 240 3 / 150 ° V

    V C A = 240 3 / - 150 ° V

    E:

    I a A = 240 / 0 ° 13,33 / - 30 ° = 18 / 30 ° A

    Da mesma forma:

    I b B = 18 / 150 ° A

    I c C = 18 / - 90 ° A

    Assim:

    W 1 = 18 240 3 c o s 0 ° = 7482,46   W

    W 2 = 18 240 3 c o s ⁡ ( - 60 ° ) = 3741,23   W

    Passo 2

  2. Supondo que:

P T = 3 P ϕ = 3 18 2 40 3 cos ⁡ - 30 ° = 11223,69   W

E temos que:

W 1 + W 2 = 11223,69   W

OK!

Resposta

  1. Item a:

    2. W 1 = 18 240 3 c o s 0 ° = 7482,46   W

    W 2 = 18 240 3 c o s ⁡ ( - 60 ° ) = 3741,23   W

  2. Sim.

Exercícios de Livros Relacionados

Considere a Figura 12.55 e elabore um problema para ajudar outros estudantes a entender melhor fontes em delta equilibradas que alimentam cargas em estrela equilibradas.
Na Figura 12.56, o valor RMS da tensão de linha é 208 V. Determine a potência média liberada para a carga.
Uma carga conectada em triângulo equilibrada é alimentada por uma fonte trifásica de 60H z com tensão de linha igual a 240V . Cada fase da carga absorve 6k W com fator de potência igual a 0,8 (atrasad
Três impedâncias iguais, de 60 + j30 Ω cada, são ligadas em triângulo a um circuito trifásico de 230 V RMS. Outras três impedâncias iguais, de 40 + j10 Ω cada, são ligadas em estrela no mesmo circuito
Uma fonte trifásica libera 4,8k V A para uma carga conectada em estrela com tensão de fase igual a208V e fator de potência 0,9 (atrasado). Calcule a corrente e a tensão de linha da fonte.