Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 10.Problemas - Ex. 26
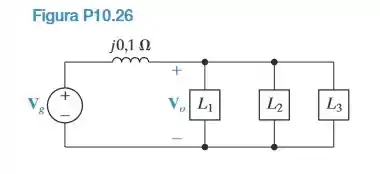
As três cargas em paralelo no circuito da Figura P10.26 podem ser descritas da seguinte forma: a carga 1 está absorvendo uma potência média de 6 kW e fornecendo uma potência reativa de 8 kVARs; a carga 2 está absorvendo uma potência média de 9 kW e uma potência reativa de 3 kVARs; a carga 3 consiste em um resistor de 25 V em paralelo com uma reatância indutiva de -5 V. Determine o valor eficaz do módulo de e seu ângulo de fase, se .
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Vamos lá, a potência complexa da carga 1 é igual a
Determinando a corrente (valor RMS) que está fluindo na primeira carga, nós temos que
Simplificando, nós obtemos o seguinte resultado
Portanto, é igual a
Transformando em fasores,
Passo 2
A potência complexa de é dada por
Determinando a corrente (valor RMS) fluindo através da segunda carga
Rearranjando,
Portanto,
Transformando em fasores
Passo 3
Determinando a impedância equivalente da carga
Determinando a corrente fluindo atráves da terceira carga
Logo
E em fasor
Determinando a corrente fornecida pela fonte de tensão,
Substituindo os valores, nós temos que
Passo 4
Determinando a tensão aplicada na impedância da linha,
Com isso o valor RMS de
Substituindo os valores, nós temos que
Logo
Com isso, em fasores é igual a